Convex vs nonconvex approaches for sparse estimation: GLasso, Multiple Kernel Learning and Hyperparameter GLasso
Paper and Code
Feb 27, 2013
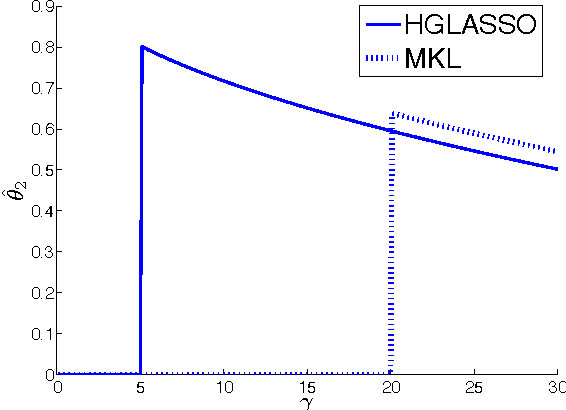
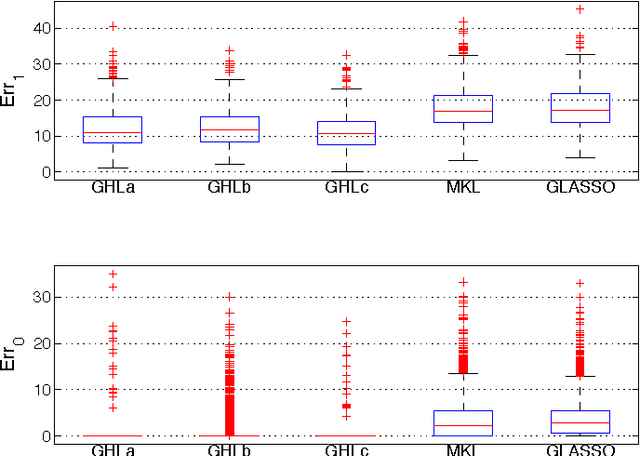

The popular Lasso approach for sparse estimation can be derived via marginalization of a joint density associated with a particular stochastic model. A different marginalization of the same probabilistic model leads to a different non-convex estimator where hyperparameters are optimized. Extending these arguments to problems where groups of variables have to be estimated, we study a computational scheme for sparse estimation that differs from the Group Lasso. Although the underlying optimization problem defining this estimator is non-convex, an initialization strategy based on a univariate Bayesian forward selection scheme is presented. This also allows us to define an effective non-convex estimator where only one scalar variable is involved in the optimization process. Theoretical arguments, independent of the correctness of the priors entering the sparse model, are included to clarify the advantages of this non-convex technique in comparison with other convex estimators. Numerical experiments are also used to compare the performance of these approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge