Convex and Nonconvex Optimization Are Both Minimax-Optimal for Noisy Blind Deconvolution
Paper and Code
Aug 04, 2020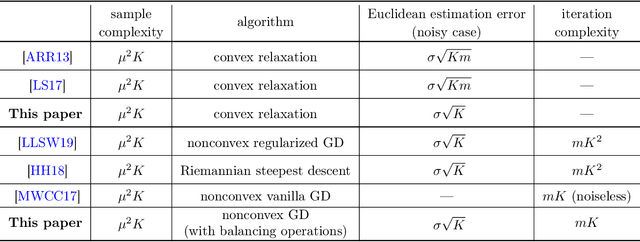
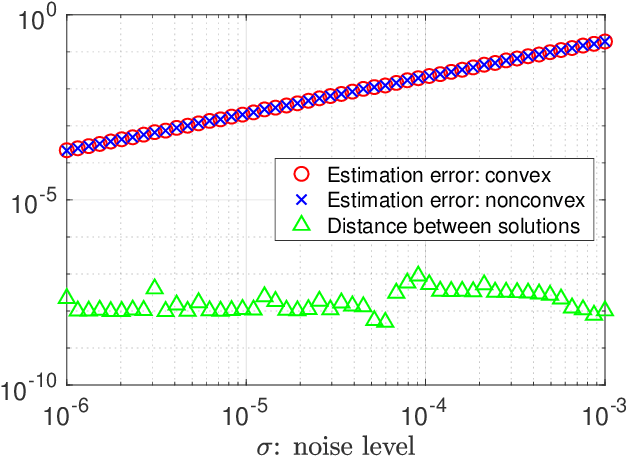
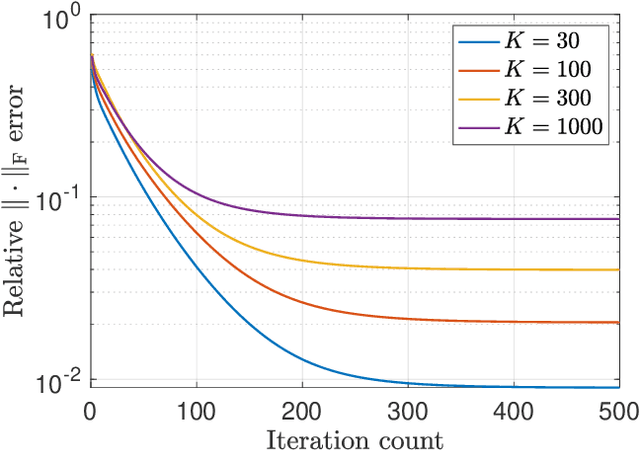
We investigate the effectiveness of convex relaxation and nonconvex optimization in solving bilinear systems of equations (a.k.a. blind deconvolution under a subspace model). Despite the wide applicability, the theoretical understanding about these two paradigms remains largely inadequate in the presence of noise. The current paper makes two contributions by demonstrating that: (1) convex relaxation achieves minimax-optimal statistical accuracy vis-\`a-vis random noise, and (2) a two-stage nonconvex algorithm attains minimax-optimal accuracy within a logarithmic number of iterations. Both results improve upon the state-of-the-art results by some factors that scale polynomially in the problem dimension.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge