Convergence of Gradient Descent on Separable Data

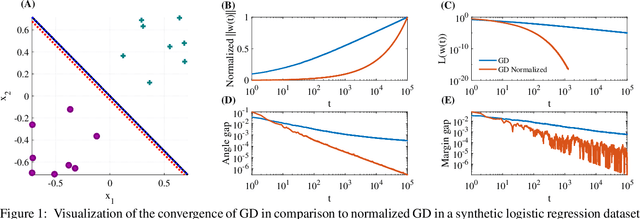
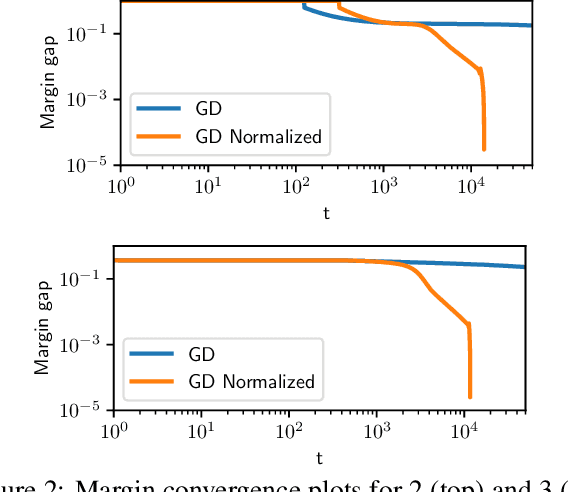
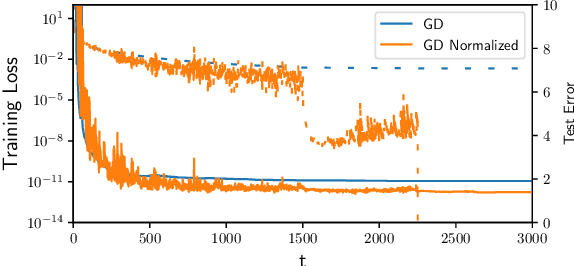
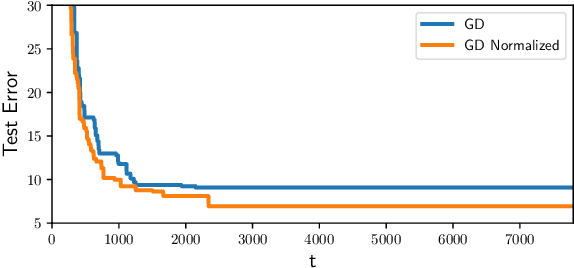
The implicit bias of gradient descent is not fully understood even in simple linear classification tasks (e.g., logistic regression). Soudry et al. (2018) studied this bias on separable data, where there are multiple solutions that correctly classify the data. It was found that, when optimizing monotonically decreasing loss functions with exponential tails using gradient descent, the linear classifier specified by the gradient descent iterates converge to the $L_2$ max margin separator. However, the convergence rate to the maximum margin solution with fixed step size was found to be extremely slow: $1/\log(t)$. Here we examine how the convergence is influenced by using different loss functions and by using variable step sizes. First, we calculate the convergence rate for loss functions with poly-exponential tails near $\exp(-u^{\nu})$. We prove that $\nu=1$ yields the optimal convergence rate in the range $\nu>0.25$. Based on further analysis we conjecture that this remains the optimal rate for $\nu \leq 0.25$, and even for sub-poly-exponential tails --- until loss functions with polynomial tails no longer converge to the max margin. Second, we prove the convergence rate could be improved to $(\log t) /\sqrt{t}$ for the exponential loss, by using aggressive step sizes which compensate for the rapidly vanishing gradients.