Continuous Mean-Covariance Bandits

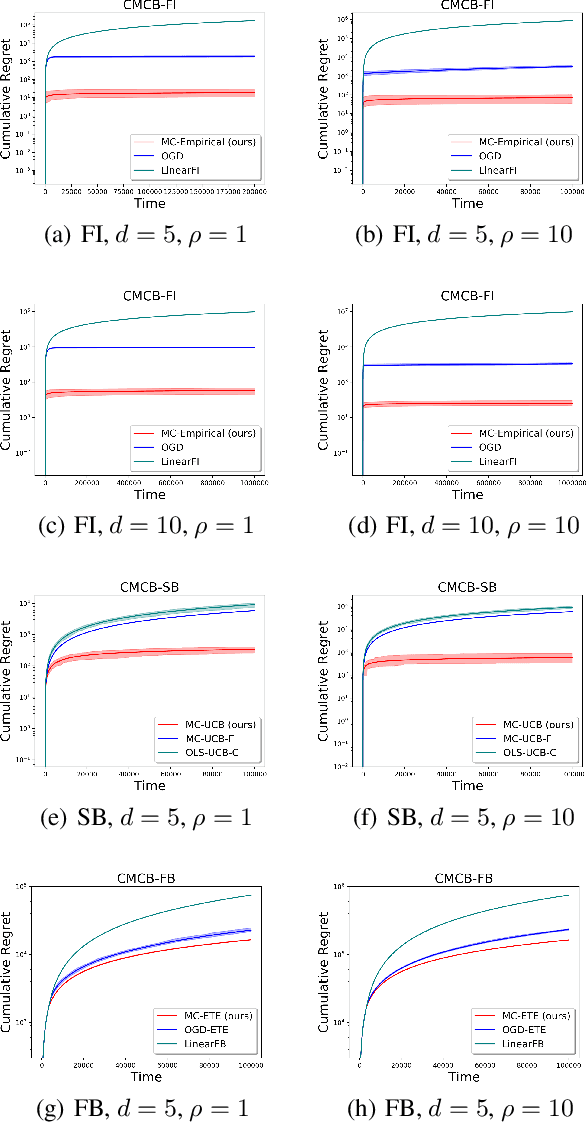
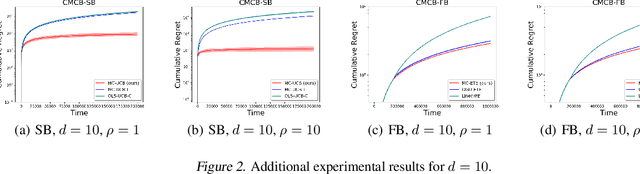
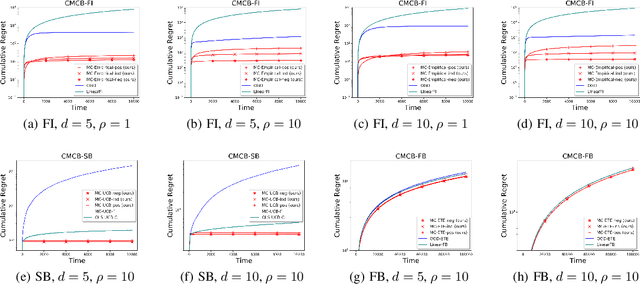
Existing risk-aware multi-armed bandit models typically focus on risk measures of individual options such as variance. As a result, they cannot be directly applied to important real-world online decision making problems with correlated options. In this paper, we propose a novel Continuous Mean-Covariance Bandit (CMCB) model to explicitly take into account option correlation. Specifically, in CMCB, there is a learner who sequentially chooses weight vectors on given options and observes random feedback according to the decisions. The agent's objective is to achieve the best trade-off between reward and risk, measured with option covariance. To capture important reward observation scenarios in practice, we consider three feedback settings, i.e., full-information, semi-bandit and full-bandit feedback. We propose novel algorithms with the optimal regrets (within logarithmic factors), and provide matching lower bounds to validate their optimalities. Our experimental results also demonstrate the superiority of the proposed algorithms. To the best of our knowledge, this is the first work that considers option correlation in risk-aware bandits and explicitly quantifies how arbitrary covariance structures impact the learning performance.