Continuous Graph Neural Networks

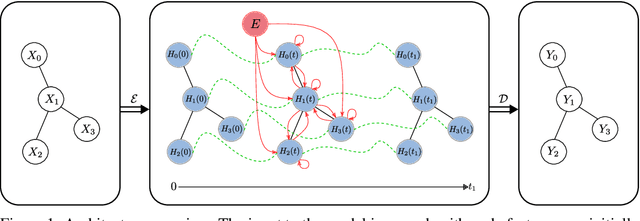
This paper builds the connection between graph neural networks and traditional dynamical systems. Existing graph neural networks essentially define a discrete dynamic on node representations with multiple graph convolution layers. We propose continuous graph neural networks (CGNN), which generalise existing graph neural networks into the continuous-time dynamic setting. The key idea is how to characterise the continuous dynamics of node representations, i.e. the derivatives of node representations w.r.t. time. Inspired by existing diffusion-based methods on graphs (e.g. PageRank and epidemic models on social networks), we define the derivatives as a combination of the current node representations, the representations of neighbors, and the initial values of the nodes. We propose and analyse different possible dynamics on graphs---including each dimension of node representations (a.k.a. the feature channel) change independently or interact with each other---both with theoretical justification. The proposed continuous graph neural networks are robust to over-smoothing and hence capture the long-range dependencies between nodes. Experimental results on the task of node classification prove the effectiveness of our proposed approach over competitive baselines.