Continual Learning with Extended Kronecker-factored Approximate Curvature
Paper and Code
Apr 16, 2020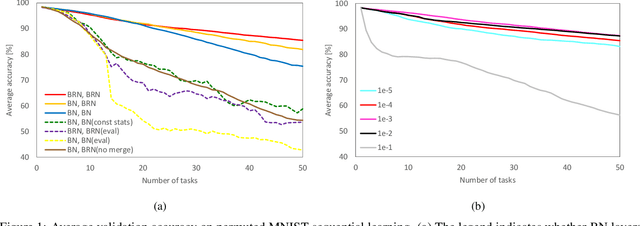
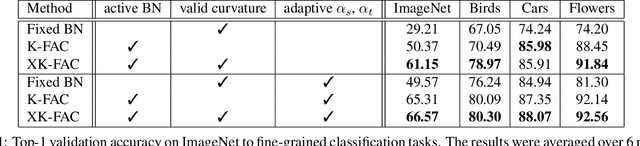
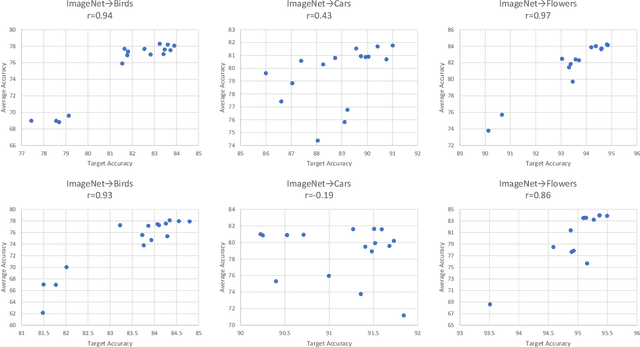
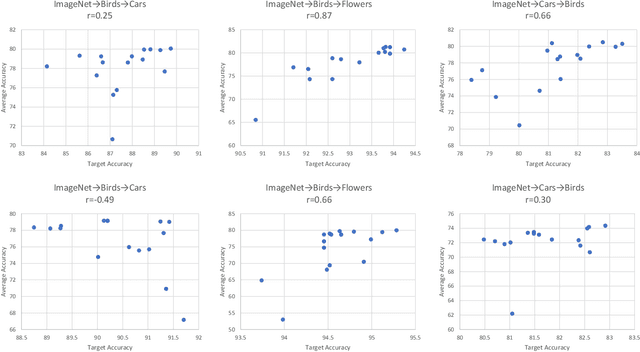
We propose a quadratic penalty method for continual learning of neural networks that contain batch normalization (BN) layers. The Hessian of a loss function represents the curvature of the quadratic penalty function, and a Kronecker-factored approximate curvature (K-FAC) is used widely to practically compute the Hessian of a neural network. However, the approximation is not valid if there is dependence between examples, typically caused by BN layers in deep network architectures. We extend the K-FAC method so that the inter-example relations are taken into account and the Hessian of deep neural networks can be properly approximated under practical assumptions. We also propose a method of weight merging and reparameterization to properly handle statistical parameters of BN, which plays a critical role for continual learning with BN, and a method that selects hyperparameters without source task data. Our method shows better performance than baselines in the permuted MNIST task with BN layers and in sequential learning from the ImageNet classification task to fine-grained classification tasks with ResNet-50, without any explicit or implicit use of source task data for hyperparameter selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge