Continual Learning of Generative Models with Limited Data: From Wasserstein-1 Barycenter to Adaptive Coalescence

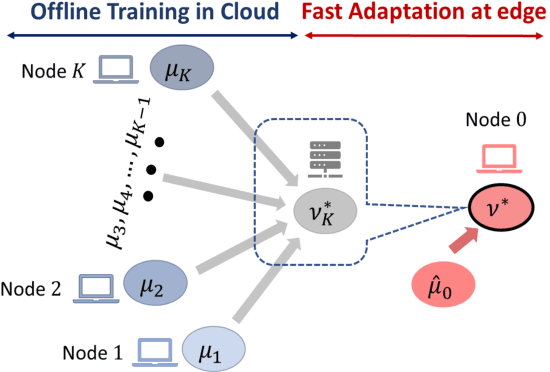
Learning generative models is challenging for a network edge node with limited data and computing power. Since tasks in similar environments share model similarity, it is plausible to leverage pre-trained generative models from the cloud or other edge nodes. Appealing to optimal transport theory tailored towards Wasserstein-1 generative adversarial networks (WGAN), this study aims to develop a framework which systematically optimizes continual learning of generative models using local data at the edge node while exploiting adaptive coalescence of pre-trained generative models. Specifically, by treating the knowledge transfer from other nodes as Wasserstein balls centered around their pre-trained models, continual learning of generative models is cast as a constrained optimization problem, which is further reduced to a Wasserstein-1 barycenter problem. A two-stage approach is devised accordingly: 1) The barycenters among the pre-trained models are computed offline, where displacement interpolation is used as the theoretic foundation for finding adaptive barycenters via a "recursive" WGAN configuration; 2) the barycenter computed offline is used as meta-model initialization for continual learning and then fast adaptation is carried out to find the generative model using the local samples at the target edge node. Finally, a weight ternarization method, based on joint optimization of weights and threshold for quantization, is developed to compress the generative model further.