Constraint Handling in Continuous-Time DDP-Based Model Predictive Control
Paper and Code
Jan 15, 2021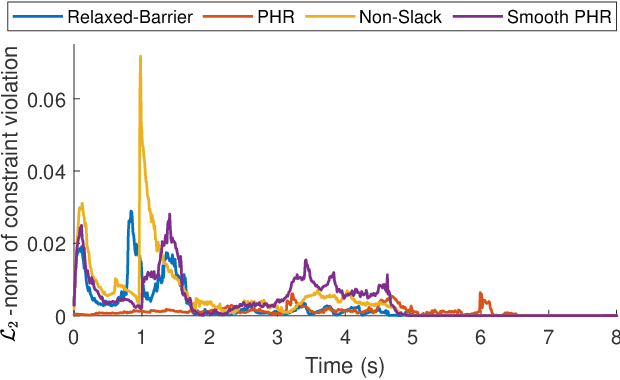
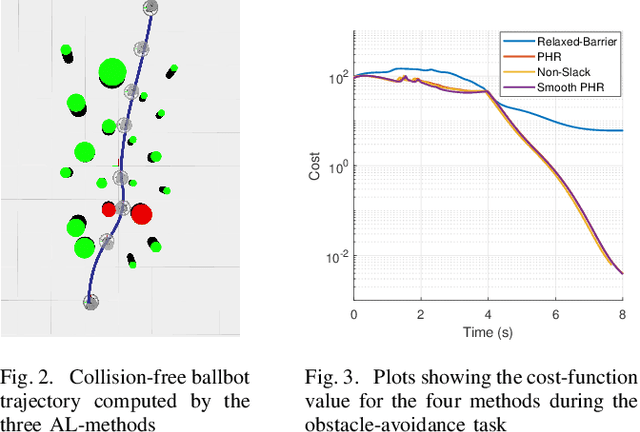
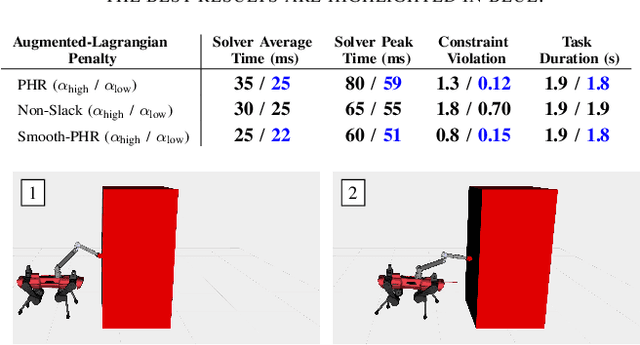
The Sequential Linear Quadratic (SLQ) algorithm is a continuous-time variant of the well-known Differential Dynamic Programming (DDP) technique with a Gauss-Newton Hessian approximation. This family of methods has gained popularity in the robotics community due to its efficiency in solving complex trajectory optimization problems. However, one major drawback of DDP-based formulations is their inability to properly incorporate path constraints. In this paper, we address this issue by devising a constrained SLQ algorithm that handles a mixture of constraints with a previously implemented projection technique and a new augmented-Lagrangian approach. By providing an appropriate multiplier update law, and by solving a single inner and outer loop iteration, we are able to retrieve suboptimal solutions at rates suitable for real-time model-predictive control applications. We particularly focus on the inequality-constrained case, where three augmented-Lagrangian penalty functions are introduced, along with their corresponding multiplier update rules. These are then benchmarked against a relaxed log-barrier formulation in a cart-pole swing up example, an obstacle-avoidance task, and an object-pushing task with a quadrupedal mobile manipulator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge