Constrained Classification and Ranking via Quantiles
Paper and Code
Feb 28, 2018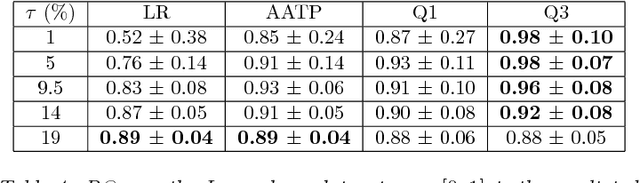
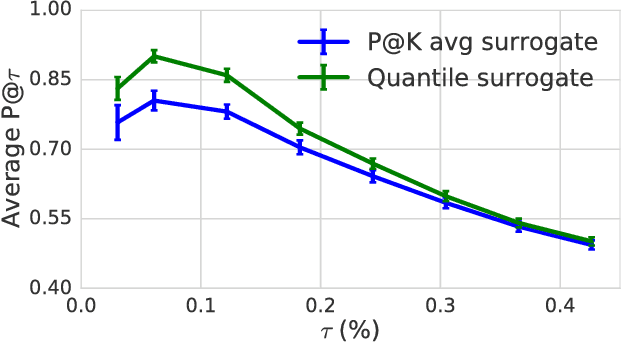
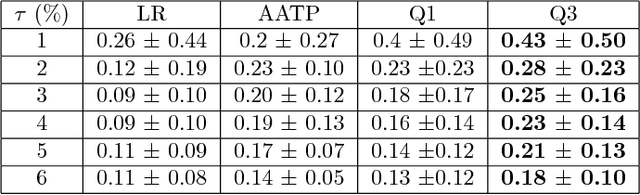
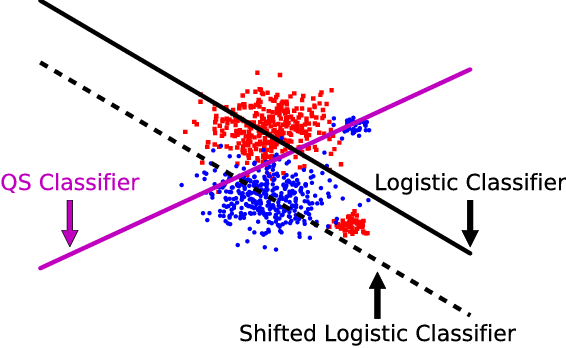
In most machine learning applications, classification accuracy is not the primary metric of interest. Binary classifiers which face class imbalance are often evaluated by the $F_\beta$ score, area under the precision-recall curve, Precision at K, and more. The maximization of many of these metrics can be expressed as a constrained optimization problem, where the constraint is a function of the classifier's predictions. In this paper we propose a novel framework for learning with constraints that can be expressed as a predicted positive rate (or negative rate) on a subset of the training data. We explicitly model the threshold at which a classifier must operate to satisfy the constraint, yielding a surrogate loss function which avoids the complexity of constrained optimization. The method is model-agnostic and only marginally more expensive than minimization of the unconstrained loss. Experiments on a variety of benchmarks show competitive performance relative to existing baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge