Consistency regularization-based Deep Polynomial Chaos Neural Network Method for Reliability Analysis

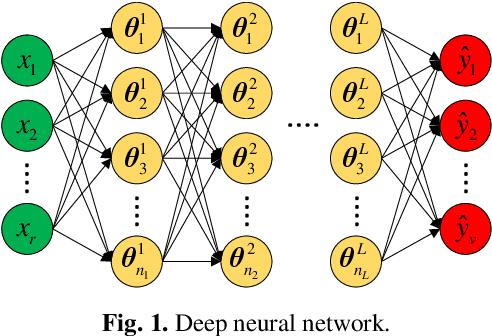
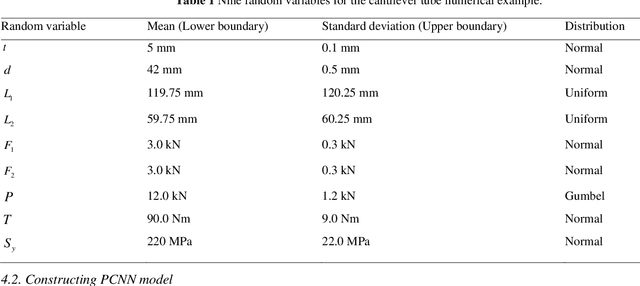
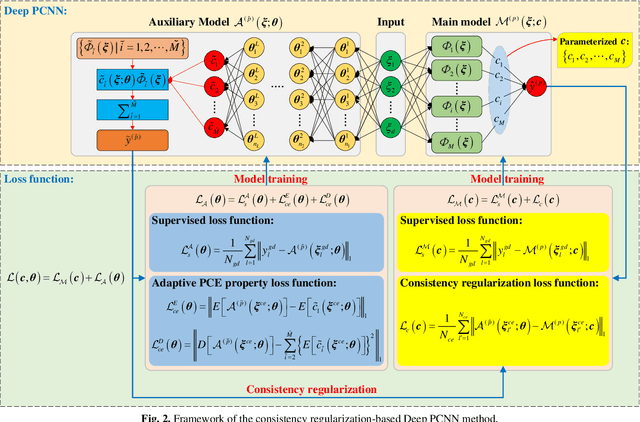
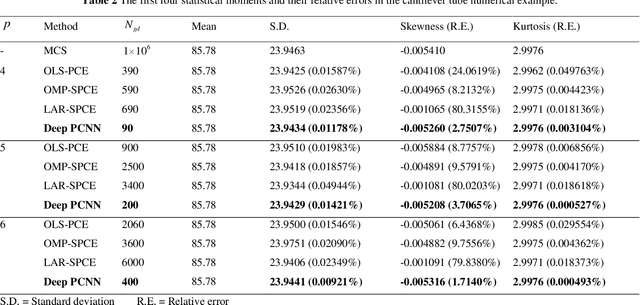
Polynomial chaos expansion (PCE) is a powerful surrogate model-based reliability analysis method. Generally, a PCE model with a higher expansion order is usually required to obtain an accurate surrogate model for some complex non-linear stochastic systems. However, the high-order PCE increases the number of labeled data required for solving the expansion coefficients. To alleviate this problem, this paper proposes a consistency regularization-based deep polynomial chaos neural network (Deep PCNN) method, including the low-order adaptive PCE model (the auxiliary model) and the high-order polynomial chaos neural network (the main model). The expansion coefficients of the main model are parameterized into the learnable weights of the polynomial chaos neural network, realizing iterative learning of expansion coefficients to obtain more accurate high-order PCE models. The auxiliary model uses a proposed consistency regularization loss function to assist in training the main model. The consistency regularization-based Deep PCNN method can significantly reduce the number of labeled data in constructing a high-order PCE model without losing accuracy by using few labeled data and abundant unlabeled data. A numerical example validates the effectiveness of the consistency regularization-based Deep PCNN method, and then this method is applied to analyze the reliability of two aerospace engineering systems.