Consistency of a Recurrent Language Model With Respect to Incomplete Decoding
Paper and Code
Feb 06, 2020
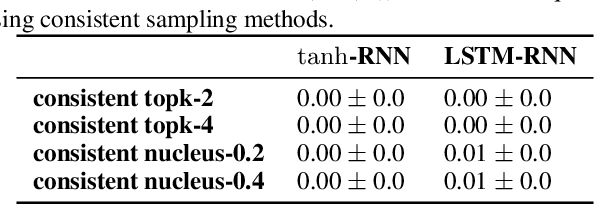


Despite strong performance on a variety of tasks, neural sequence models trained with maximum likelihood have been shown to exhibit issues such as length bias and degenerate repetition. We study the related issue of receiving infinite-length sequences from a recurrent language model when using common decoding algorithms. To analyze this issue, we first define inconsistency of a decoding algorithm, meaning that the algorithm can yield an infinite-length sequence that has zero probability under the model. We prove that commonly used incomplete decoding algorithms - greedy search, beam search, top-k sampling, and nucleus sampling - are inconsistent, despite the fact that recurrent language models are trained to produce sequences of finite length. Based on these insights, we propose two remedies which address inconsistency: consistent variants of top-k and nucleus sampling, and a self-terminating recurrent language model. Empirical results show that inconsistency occurs in practice, and that the proposed methods prevent inconsistency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge