Connecting First and Second Order Recurrent Networks with Deterministic Finite Automata
Paper and Code
Nov 12, 2019

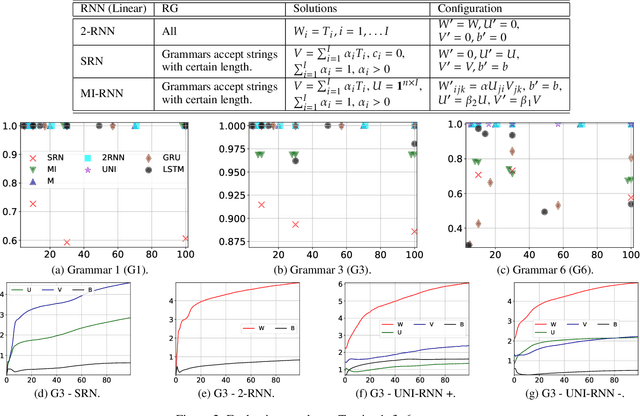
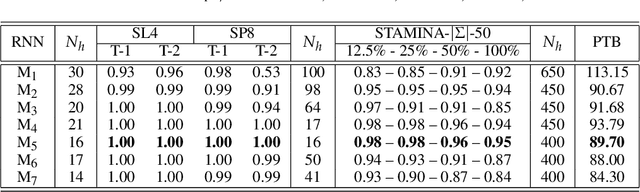
We propose an approach that connects recurrent networks with different orders of hidden interaction with regular grammars of different levels of complexity. We argue that the correspondence between recurrent networks and formal computational models gives understanding to the analysis of the complicated behaviors of recurrent networks. We introduce an entropy value that categorizes all regular grammars into three classes with different levels of complexity, and show that several existing recurrent networks match grammars from either all or partial classes. As such, the differences between regular grammars reveal the different properties of these models. We also provide a unification of all investigated recurrent networks. Our evaluation shows that the unified recurrent network has improved performance in learning grammars, and demonstrates comparable performance on a real-world dataset with more complicated models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge