Conjugate Gradient Adaptive Learning with Tukey's Biweight M-Estimate
Paper and Code
Mar 19, 2022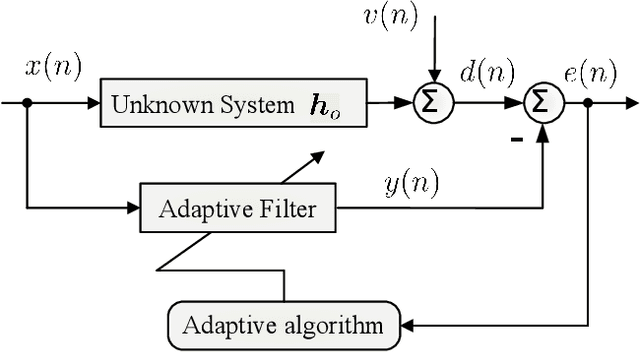
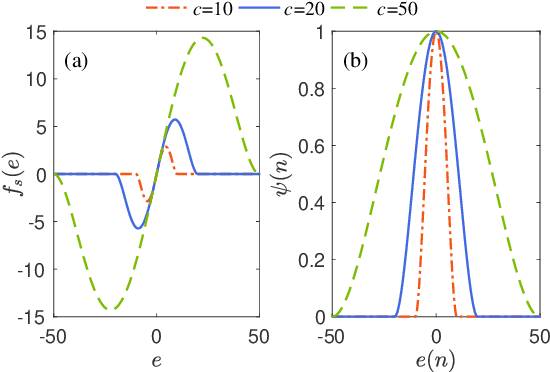
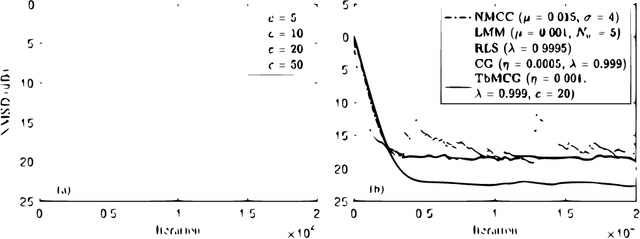
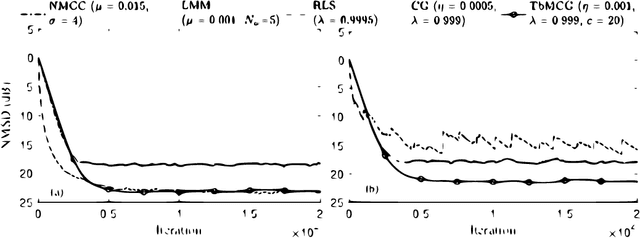
We propose a novel M-estimate conjugate gradient (CG) algorithm, termed Tukey's biweight M-estimate CG (TbMCG), for system identification in impulsive noise environments. In particular, the TbMCG algorithm can achieve a faster convergence while retaining a reduced computational complexity as compared to the recursive least-squares (RLS) algorithm. Specifically, the Tukey's biweight M-estimate incorporates a constraint into the CG filter to tackle impulsive noise environments. Moreover, the convergence behavior of the TbMCG algorithm is analyzed. Simulation results confirm the excellent performance of the proposed TbMCG algorithm for system identification and active noise control applications.
* 16 pages, 6 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge