Confidence Calibration with Bounded Error Using Transformations

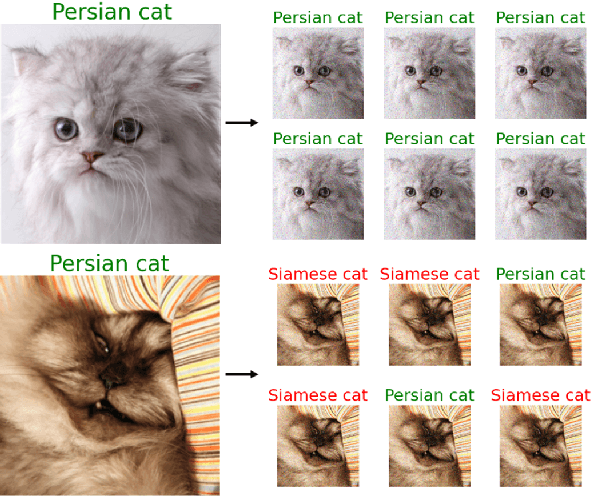
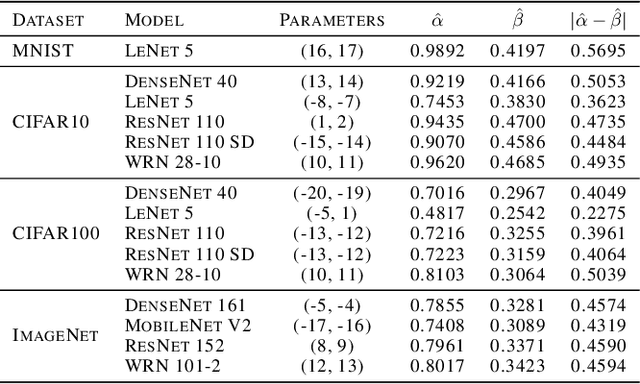
As machine learning techniques become widely adopted in new domains, especially in safety-critical systems such as autonomous vehicles, it is crucial to provide accurate output uncertainty estimation. As a result, many approaches have been proposed to calibrate neural networks to accurately estimate the likelihood of misclassification. However, while these methods achieve low expected calibration error (ECE), few techniques provide theoretical performance guarantees on the calibration error (CE). In this paper, we introduce Hoki, a novel calibration algorithm with a theoretical bound on the CE. Hoki works by transforming the neural network logits and/or inputs and recursively performing calibration leveraging the information from the corresponding change in the output. We provide a PAC-like bounds on CE that is shown to decrease with the number of samples used for calibration, and increase proportionally with ECE and the number of discrete bins used to calculate ECE. We perform experiments on multiple datasets, including ImageNet, and show that the proposed approach generally outperforms state-of-the-art calibration algorithms across multiple datasets and models - providing nearly an order or magnitude improvement in ECE on ImageNet. In addition, Hoki is fast algorithm which is comparable to temperature scaling in terms of learning time.