Concentration of Contractive Stochastic Approximation: Additive and Multiplicative Noise

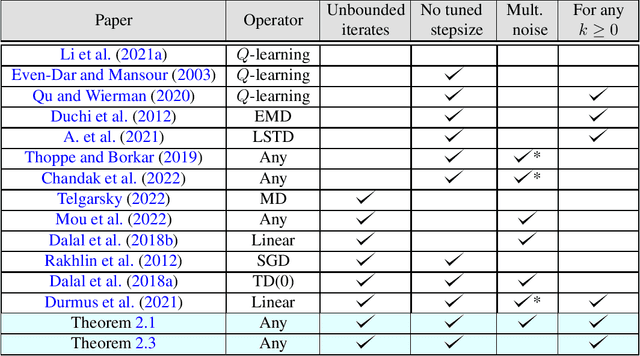
In this work, we study the concentration behavior of a stochastic approximation (SA) algorithm under a contractive operator with respect to an arbitrary norm. We consider two settings where the iterates are potentially unbounded: (1) bounded multiplicative noise, and (2) additive sub-Gaussian noise. We obtain maximal concentration inequalities on the convergence errors, and show that these errors have sub-Gaussian tails in the additive noise setting, and super-polynomial tails (faster than polynomial decay) in the multiplicative noise setting. In addition, we provide an impossibility result showing that it is in general not possible to achieve sub-exponential tails for SA with multiplicative noise. To establish these results, we develop a novel bootstrapping argument that involves bounding the moment generating function of the generalized Moreau envelope of the error and the construction of an exponential supermartingale to enable using Ville's maximal inequality. To demonstrate the applicability of our theoretical results, we use them to provide maximal concentration bounds for a large class of reinforcement learning algorithms, including but not limited to on-policy TD-learning with linear function approximation, off-policy TD-learning with generalized importance sampling factors, and $Q$-learning. To the best of our knowledge, super-polynomial concentration bounds for off-policy TD-learning have not been established in the literature due to the challenge of handling the combination of unbounded iterates and multiplicative noise.