Compressed Subspace Learning Based on Canonical Angle Preserving Property
Paper and Code
Jul 24, 2019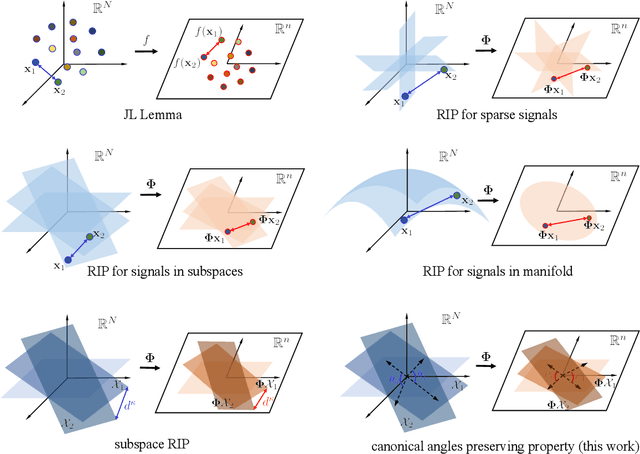
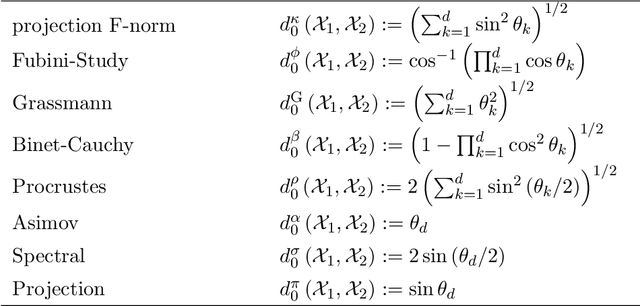
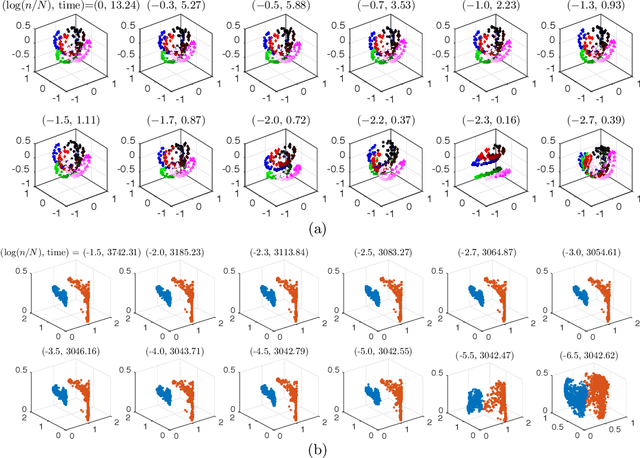
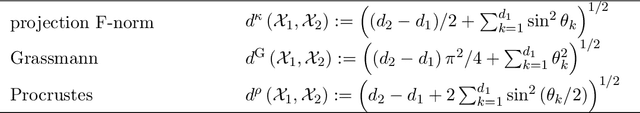
Union of Subspaces (UoS) is a popular model to describe the underlying low-dimensional structure of data. The fine details of UoS structure can be described in terms of canonical angles (also known as principal angles) between subspaces, which is a well-known characterization for relative subspace positions. In this paper, we prove that random projection with the so-called Johnson-Lindenstrauss (JL) property approximately preserves canonical angles between subspaces with overwhelming probability. This result indicates that random projection approximately preserves the UoS structure. Inspired by this result, we propose a framework of Compressed Subspace Learning (CSL), which enables to extract useful information from the UoS structure of data in a greatly reduced dimension. We demonstrate the effectiveness of CSL in various subspace-related tasks such as subspace visualization, active subspace detection, and subspace clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge