Communication-Efficient Distributed SVD via Local Power Iterations
Paper and Code
Feb 19, 2020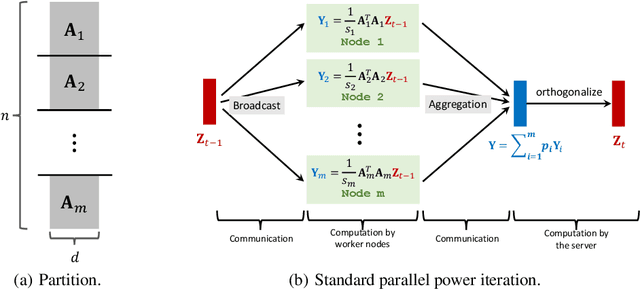

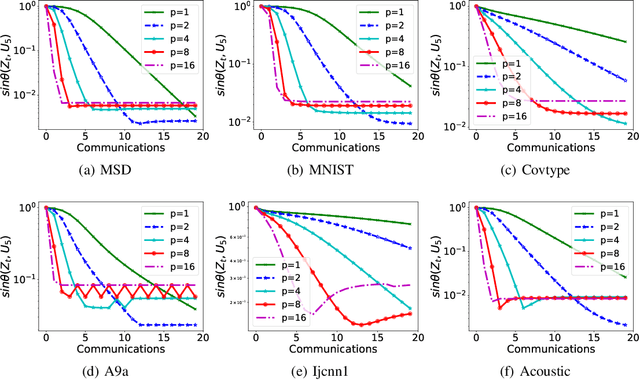
We study the distributed computing of the truncated singular value decomposition (SVD). We develop an algorithm that we call \texttt{LocalPower} for improving the communication efficiency. Specifically, we uniformly partition the dataset among $m$ nodes and alternate between multiple (precisely $p$) local power iterations and one global aggregation. We theoretically show that under certain assumptions, \texttt{LocalPower} lowers the required number of communications by a factor of $p$ to reach a certain accuracy. We also show that the strategy of periodically decaying $p$ helps improve the performance of \texttt{LocalPower}. We conduct experiments to demonstrate the effectiveness of \texttt{LocalPower}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge