Communication-efficient distributed SGD with Sketching
Paper and Code
Mar 12, 2019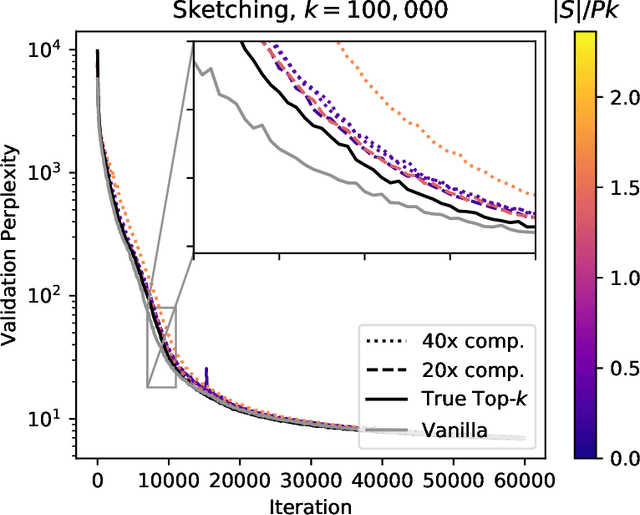


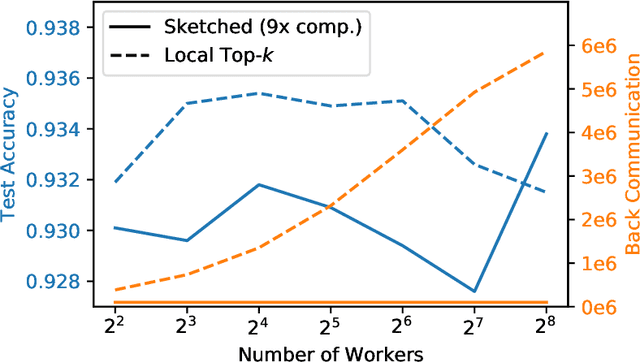
Large-scale distributed training of neural networks is often limited by network bandwidth, wherein the communication time overwhelms the local computation time. Motivated by the success of sketching methods in sub-linear/streaming algorithms, we propose a sketching-based approach to minimize the communication costs between nodes without losing accuracy. In our proposed method, workers in a distributed, synchronous training setting send sketches of their gradient vectors to the parameter server instead of the full gradient vector. Leveraging the theoretical properties of sketches, we show that this method recovers the favorable convergence guarantees of single-machine top-$k$ SGD. Furthermore, when applied to a model with $d$ dimensions on $W$ workers, our method requires only $\Theta(kW)$ bytes of communication, compared to $\Omega(dW)$ for vanilla distributed SGD. To validate our method, we run experiments using a residual network trained on the CIFAR-10 dataset. We achieve no drop in validation accuracy with a compression ratio of 4, or about 1 percentage point drop with a compression ratio of 8. We also demonstrate that our method scales to many workers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge