Communication Compression for Decentralized Learning with Operator Splitting Methods
Paper and Code
May 08, 2022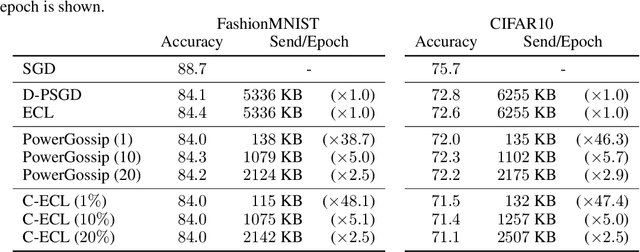
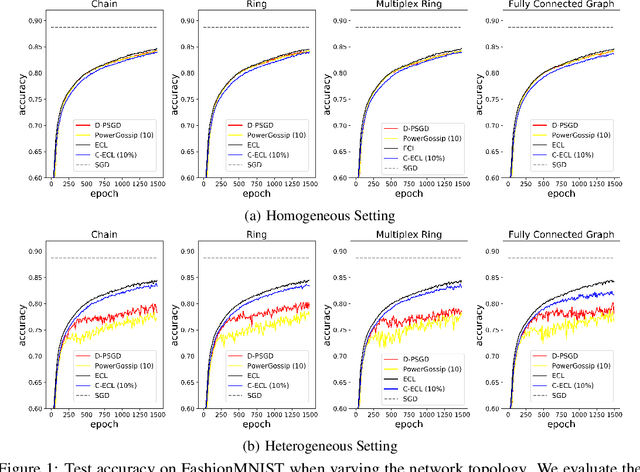
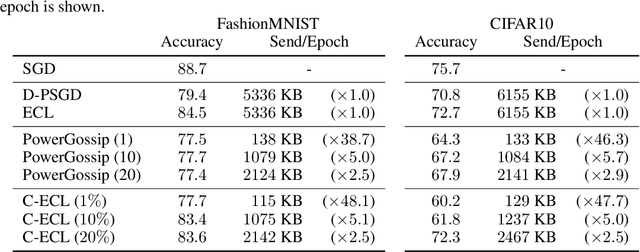
In decentralized learning, operator splitting methods using a primal-dual formulation (e.g., the Edge-Consensus Learning (ECL)) has been shown to be robust to heterogeneous data and has attracted significant attention in recent years. However, in the ECL, a node needs to exchange dual variables with its neighbors. These exchanges incur significant communication costs. For the Gossip-based algorithms, many compression methods have been proposed, but these Gossip-based algorithm do not perform well when the data distribution held by each node is statistically heterogeneous. In this work, we propose the novel framework of the compression methods for the ECL, called the Communication Compressed ECL (C-ECL). Specifically, we reformulate the update formulas of the ECL, and propose to compress the update values of the dual variables. We demonstrate experimentally that the C-ECL can achieve a nearly equivalent performance with fewer parameter exchanges than the ECL. Moreover, we demonstrate that the C-ECL is more robust to heterogeneous data than the Gossip-based algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge