Communication Acceleration of Local Gradient Methods via an Accelerated Primal-Dual Algorithm with Inexact Prox
Paper and Code
Jul 08, 2022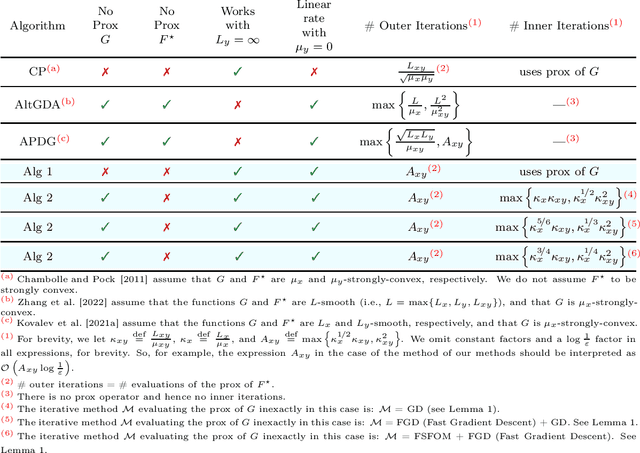
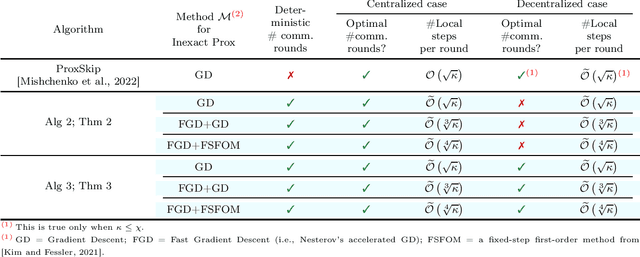
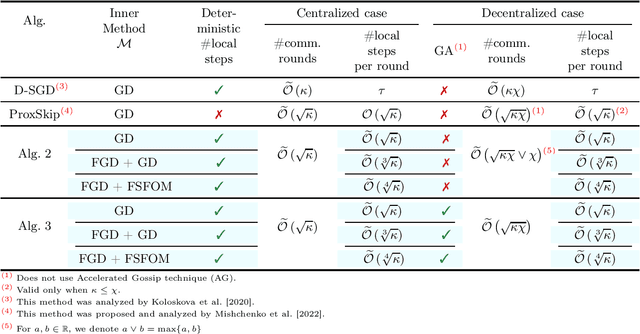
Inspired by a recent breakthrough of Mishchenko et al (2022), who for the first time showed that local gradient steps can lead to provable communication acceleration, we propose an alternative algorithm which obtains the same communication acceleration as their method (ProxSkip). Our approach is very different, however: it is based on the celebrated method of Chambolle and Pock (2011), with several nontrivial modifications: i) we allow for an inexact computation of the prox operator of a certain smooth strongly convex function via a suitable gradient-based method (e.g., GD, Fast GD or FSFOM), ii) we perform a careful modification of the dual update step in order to retain linear convergence. Our general results offer the new state-of-the-art rates for the class of strongly convex-concave saddle-point problems with bilinear coupling characterized by the absence of smoothness in the dual function. When applied to federated learning, we obtain a theoretically better alternative to ProxSkip: our method requires fewer local steps ($O(\kappa^{1/3})$ or $O(\kappa^{1/4})$, compared to $O(\kappa^{1/2})$ of ProxSkip), and performs a deterministic number of local steps instead. Like ProxSkip, our method can be applied to optimization over a connected network, and we obtain theoretical improvements here as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge