Combining Sampling- and Gradient-based Planning for Contact-rich Manipulation
Paper and Code
Oct 07, 2023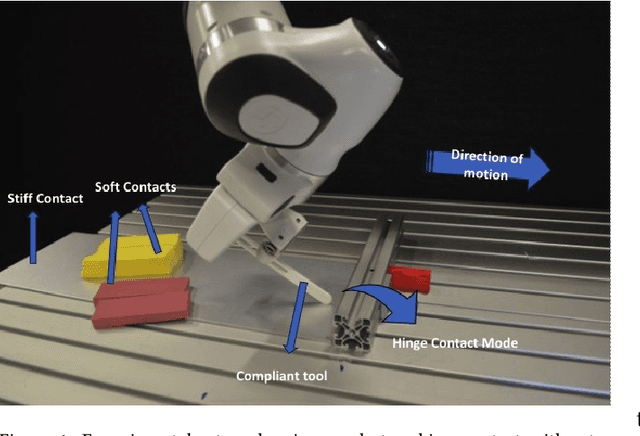
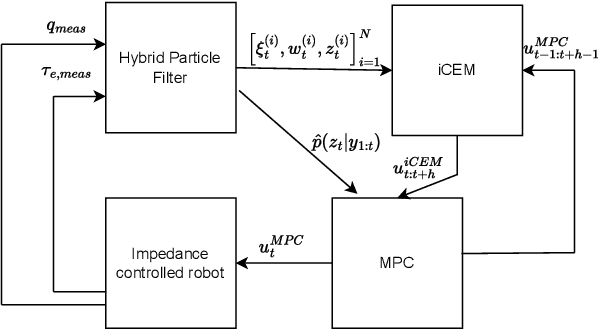
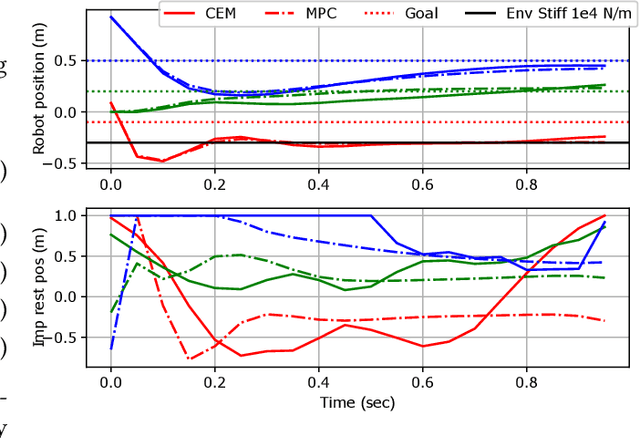
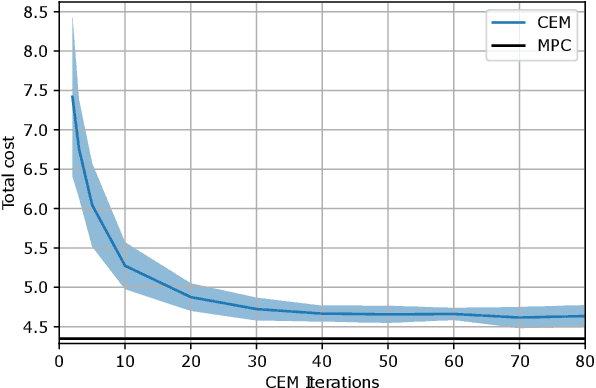
Planning over discontinuous dynamics is needed for robotics tasks like contact-rich manipulation, which presents challenges in the numerical stability and speed of planning methods when either neural network or analytical models are used. On the one hand, sampling-based planners require higher sample complexity in high-dimensional problems and cannot describe safety constraints such as force limits. On the other hand, gradient-based solvers can suffer from local optima and convergence issues when the Hessian is poorly conditioned. We propose a planning method with both sampling- and gradient-based elements, using the Cross-entropy Method to initialize a gradient-based solver, providing better search over local minima and the ability to handle explicit constraints. We show the approach allows smooth, stable contact-rich planning for an impedance-controlled robot making contact with a stiff environment, benchmarking against gradient-only MPC and CEM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge