Combining Incomplete Observational and Randomized Data for Heterogeneous Treatment Effects
Paper and Code
Oct 28, 2024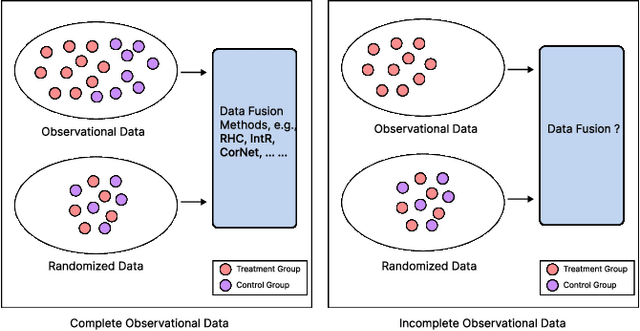
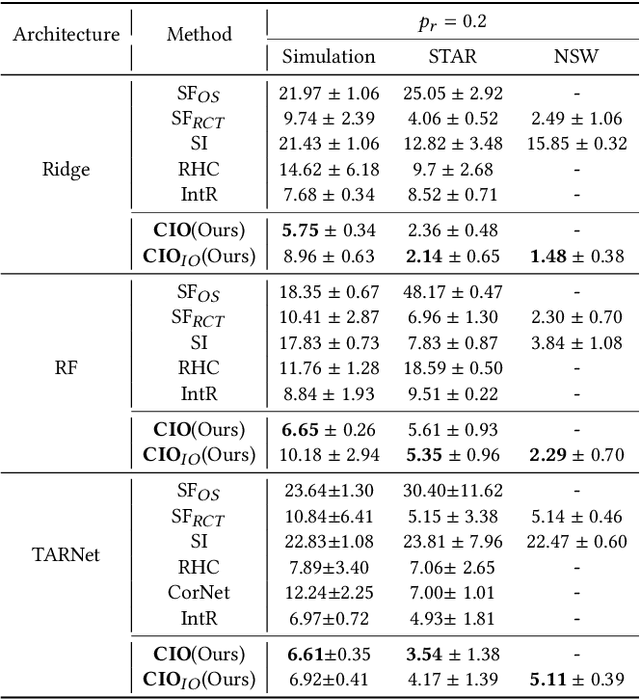
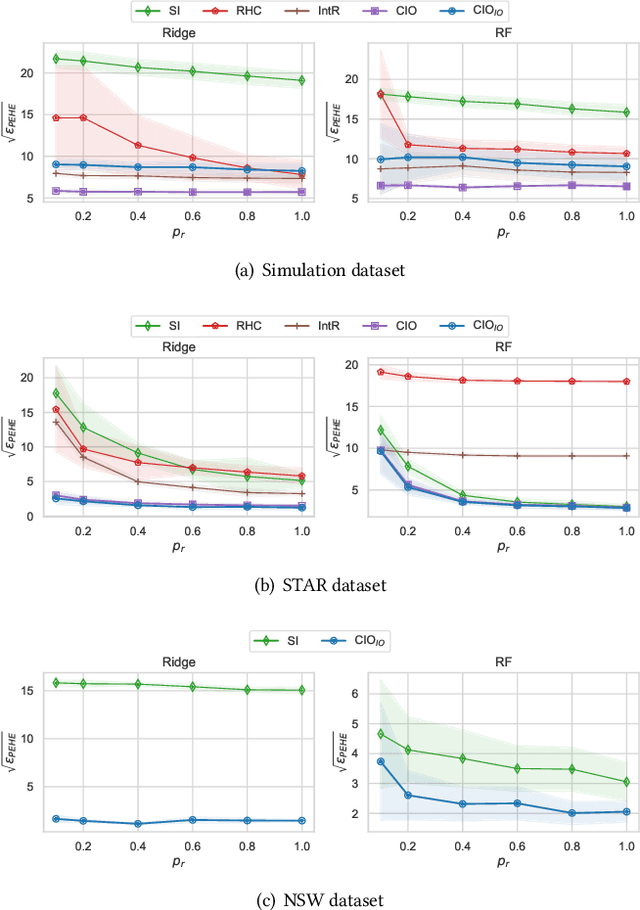
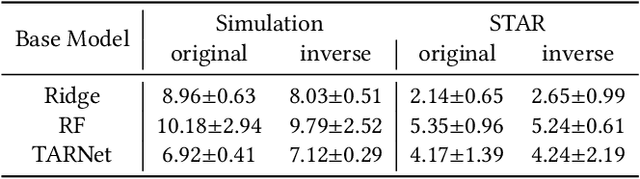
Data from observational studies (OSs) is widely available and readily obtainable yet frequently contains confounding biases. On the other hand, data derived from randomized controlled trials (RCTs) helps to reduce these biases; however, it is expensive to gather, resulting in a tiny size of randomized data. For this reason, effectively fusing observational data and randomized data to better estimate heterogeneous treatment effects (HTEs) has gained increasing attention. However, existing methods for integrating observational data with randomized data must require \textit{complete} observational data, meaning that both treated subjects and untreated subjects must be included in OSs. This prerequisite confines the applicability of such methods to very specific situations, given that including all subjects, whether treated or untreated, in observational studies is not consistently achievable. In our paper, we propose a resilient approach to \textbf{C}ombine \textbf{I}ncomplete \textbf{O}bservational data and randomized data for HTE estimation, which we abbreviate as \textbf{CIO}. The CIO is capable of estimating HTEs efficiently regardless of the completeness of the observational data, be it full or partial. Concretely, a confounding bias function is first derived using the pseudo-experimental group from OSs, in conjunction with the pseudo-control group from RCTs, via an effect estimation procedure. This function is subsequently utilized as a corrective residual to rectify the observed outcomes of observational data during the HTE estimation by combining the available observational data and the all randomized data. To validate our approach, we have conducted experiments on a synthetic dataset and two semi-synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge