Collapsed Variational Bayes Inference of Infinite Relational Model
Paper and Code
Sep 16, 2014
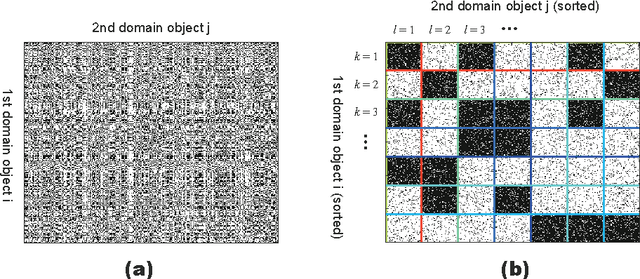
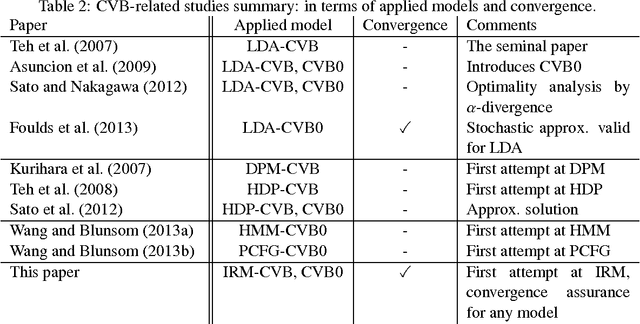

The Infinite Relational Model (IRM) is a probabilistic model for relational data clustering that partitions objects into clusters based on observed relationships. This paper presents Averaged CVB (ACVB) solutions for IRM, convergence-guaranteed and practically useful fast Collapsed Variational Bayes (CVB) inferences. We first derive ordinary CVB and CVB0 for IRM based on the lower bound maximization. CVB solutions yield deterministic iterative procedures for inferring IRM given the truncated number of clusters. Our proposal includes CVB0 updates of hyperparameters including the concentration parameter of the Dirichlet Process, which has not been studied in the literature. To make the CVB more practically useful, we further study the CVB inference in two aspects. First, we study the convergence issues and develop a convergence-guaranteed algorithm for any CVB-based inferences called ACVB, which enables automatic convergence detection and frees non-expert practitioners from difficult and costly manual monitoring of inference processes. Second, we present a few techniques for speeding up IRM inferences. In particular, we describe the linear time inference of CVB0, allowing the IRM for larger relational data uses. The ACVB solutions of IRM showed comparable or better performance compared to existing inference methods in experiments, and provide deterministic, faster, and easier convergence detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge