Clustering with Fairness Constraints: A Flexible and Scalable Approach

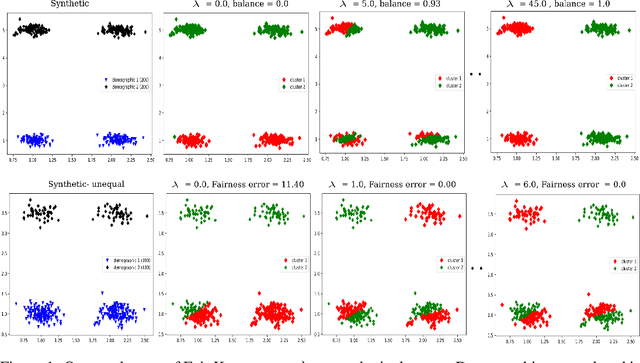
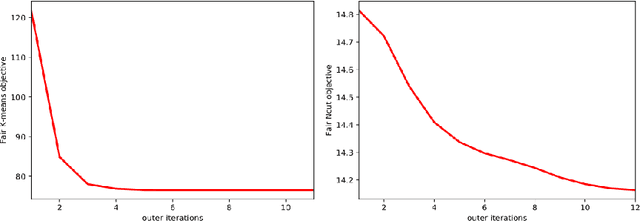
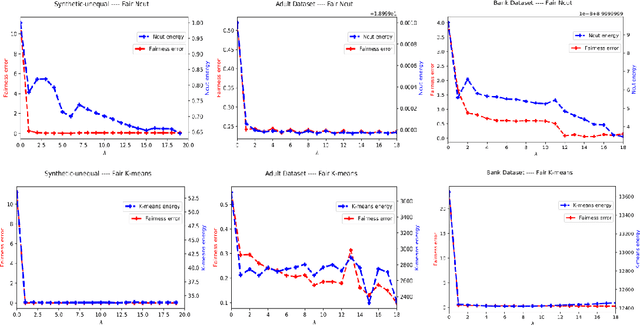
This study investigates a general variational formulation of fair clustering, which can integrate fairness constraints with a large class of clustering objectives. Unlike the existing methods, our formulation can impose any desired (target) demographic proportions within each cluster. Furthermore, it enables to control the trade-off between fairness and the clustering objective. We derive an auxiliary function (tight upper bound) of our KL-based fairness penalty via its concave-convex decomposition and Lipschitz-gradient property. Our upper bound can be optimized jointly with various clustering objectives, including both prototype-based such as K-means and graph-based such as Normalized Cut. Interestingly, at each iteration, our general fair-clustering algorithm performs an independent update for each assignment variable, while guaranteeing convergence. Therefore, it can be easily distributed for large-scale data sets. Such scalability is important as it enables to explore different trade-off levels between fairness and clustering objectives. Unlike existing fairness-constrained spectral clustering, our formulation does not need storing an affinity matrix and computing its eigenvalue decomposition. Moreover, unlike existing prototype-based methods, our experiments reveal that fairness does not come at a significant cost of the clustering objective. In fact, several of our tests showed that our fairness penalty helped to avoid weak local minima of the clustering objective (i.e., with fairness, we obtained better clustering objectives). We demonstrate the flexibility and scalability of our algorithm with comprehensive evaluations over both synthetic and real world data sets, many of which are much larger than those used in recent fair-clustering methods.