Clustering Effect of (Linearized) Adversarial Robust Models
Paper and Code
Nov 25, 2021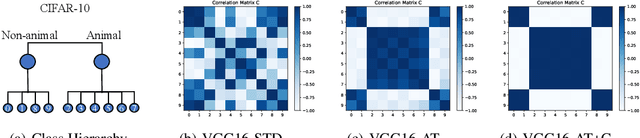
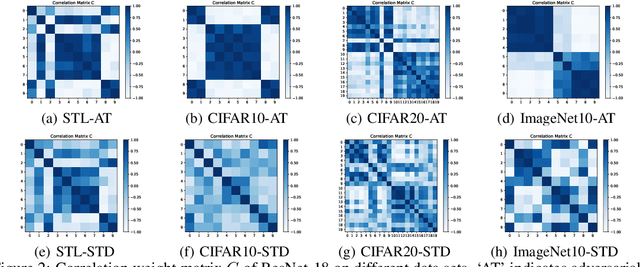
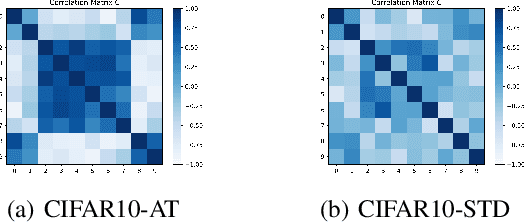
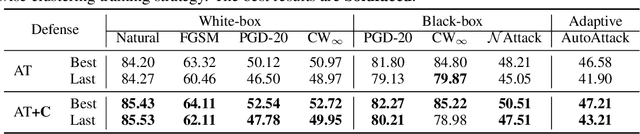
Adversarial robustness has received increasing attention along with the study of adversarial examples. So far, existing works show that robust models not only obtain robustness against various adversarial attacks but also boost the performance in some downstream tasks. However, the underlying mechanism of adversarial robustness is still not clear. In this paper, we interpret adversarial robustness from the perspective of linear components, and find that there exist some statistical properties for comprehensively robust models. Specifically, robust models show obvious hierarchical clustering effect on their linearized sub-networks, when removing or replacing all non-linear components (e.g., batch normalization, maximum pooling, or activation layers). Based on these observations, we propose a novel understanding of adversarial robustness and apply it on more tasks including domain adaption and robustness boosting. Experimental evaluations demonstrate the rationality and superiority of our proposed clustering strategy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge