Clustered Multi-Task Learning: A Convex Formulation
Paper and Code
Sep 11, 2008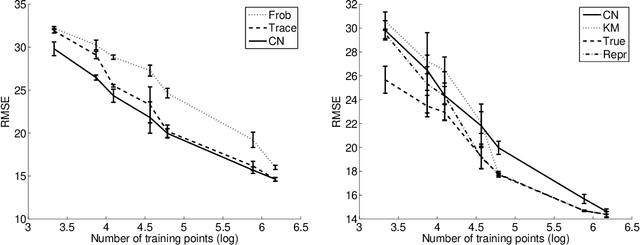
In multi-task learning several related tasks are considered simultaneously, with the hope that by an appropriate sharing of information across tasks, each task may benefit from the others. In the context of learning linear functions for supervised classification or regression, this can be achieved by including a priori information about the weight vectors associated with the tasks, and how they are expected to be related to each other. In this paper, we assume that tasks are clustered into groups, which are unknown beforehand, and that tasks within a group have similar weight vectors. We design a new spectral norm that encodes this a priori assumption, without the prior knowledge of the partition of tasks into groups, resulting in a new convex optimization formulation for multi-task learning. We show in simulations on synthetic examples and on the IEDB MHC-I binding dataset, that our approach outperforms well-known convex methods for multi-task learning, as well as related non convex methods dedicated to the same problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge