Circle detection using Discrete Differential Evolution Optimization
Paper and Code
May 28, 2014

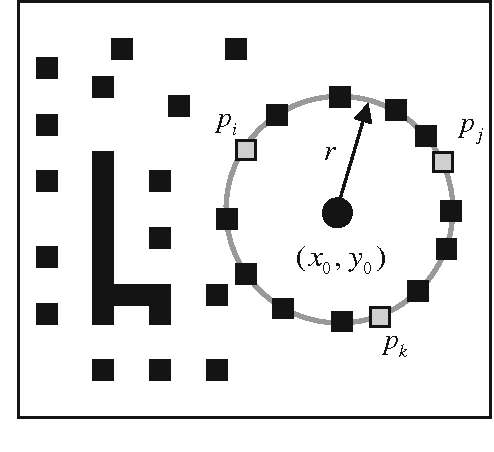
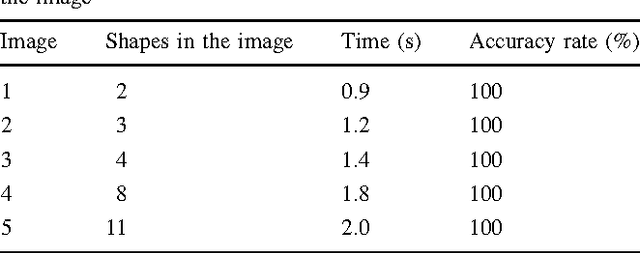
This paper introduces a circle detection method based on Differential Evolution (DE) optimization. Just as circle detection has been lately considered as a fundamental component for many computer vision algorithms, DE has evolved as a successful heuristic method for solving complex optimization problems, still keeping a simple structure and an easy implementation. It has also shown advantageous convergence properties and remarkable robustness. The detection process is considered similar to a combinational optimization problem. The algorithm uses the combination of three edge points as parameters to determine circles candidates in the scene yielding a reduction of the search space. The objective function determines if some circle candidates are actually present in the image. This paper focuses particularly on one DE-based algorithm known as the Discrete Differential Evolution (DDE), which eventually has shown better results than the original DE in particular for solving combinatorial problems. In the DDE, suitable conversion routines are incorporated into the DE, aiming to operate from integer values to real values and then getting integer values back, following the crossover operation. The final algorithm is a fast circle detector that locates circles with sub-pixel accuracy even considering complicated conditions and noisy images. Experimental results on several synthetic and natural images with varying range of complexity validate the efficiency of the proposed technique considering accuracy, speed, and robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge