Certifying Model Accuracy under Distribution Shifts
Paper and Code
Jan 28, 2022
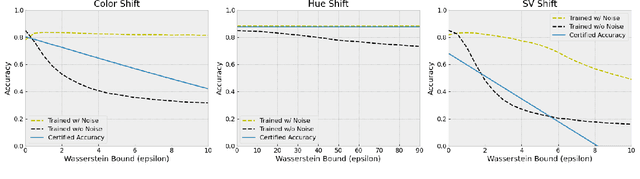
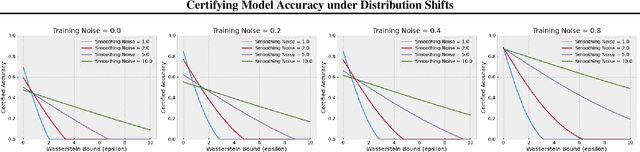
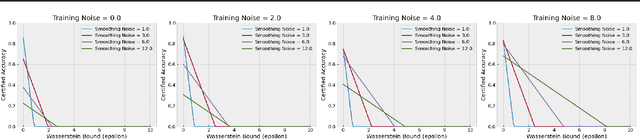
Certified robustness in machine learning has primarily focused on adversarial perturbations of the input with a fixed attack budget for each point in the data distribution. In this work, we present provable robustness guarantees on the accuracy of a model under bounded Wasserstein shifts of the data distribution. We show that a simple procedure that randomizes the input of the model within a transformation space is provably robust to distributional shifts under the transformation. Our framework allows the datum-specific perturbation size to vary across different points in the input distribution and is general enough to include fixed-sized perturbations as well. Our certificates produce guaranteed lower bounds on the performance of the model for any (natural or adversarial) shift of the input distribution within a Wasserstein ball around the original distribution. We apply our technique to: (i) certify robustness against natural (non-adversarial) transformations of images such as color shifts, hue shifts and changes in brightness and saturation, (ii) certify robustness against adversarial shifts of the input distribution, and (iii) show provable lower bounds (hardness results) on the performance of models trained on so-called "unlearnable" datasets that have been poisoned to interfere with model training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge