Certified Reinforcement Learning with Logic Guidance

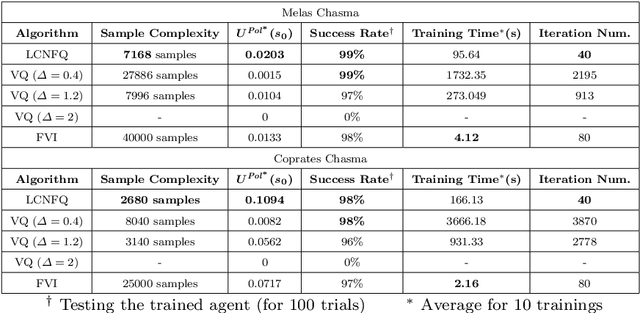
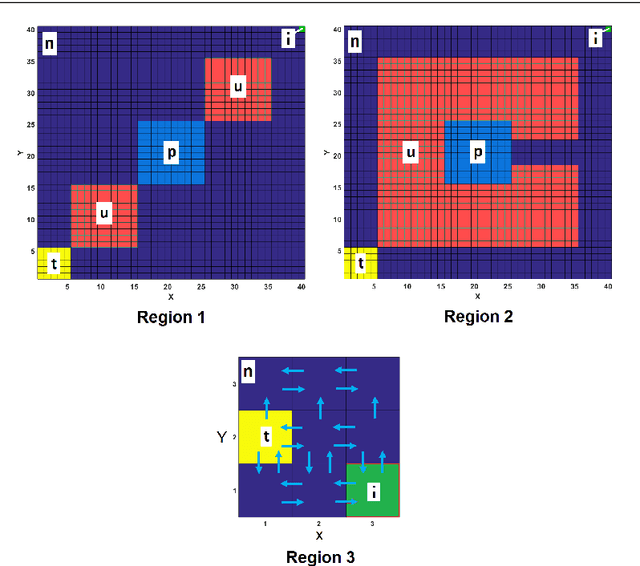
This paper proposes the first model-free Reinforcement Learning (RL) framework to synthesise policies for an unknown, and possibly continuous-state, Markov Decision Process (MDP), such that a given linear temporal property is satisfied. We convert the given property into a Limit Deterministic Buchi Automaton (LDBA), namely a finite-state machine expressing the property. Exploiting the structure of the LDBA, we shape an adaptive reward function on-the-fly, so that an RL algorithm can synthesise a policy resulting in traces that probabilistically satisfy the linear temporal property. This probability (certificate) is also calculated in parallel with learning, i.e. the RL algorithm produces a policy that is certifiably safe with respect to the property. Under the assumption that the MDP has a finite number of states, theoretical guarantees are provided on the convergence of the RL algorithm. We also show that our method produces "best available" control policies when the logical property cannot be satisfied. Whenever the MDP has a continuous state space, we empirically show that our framework finds satisfying policies, if there exist such policies. Additionally, the proposed algorithm can handle time-varying periodic environments. The performance of the proposed architecture is evaluated via a set of numerical examples and benchmarks, where we observe an improvement of one order of magnitude in the number of iterations required for the policy synthesis, compared to existing approaches whenever available.