CDVAE: Co-embedding Deep Variational Auto Encoder for Conditional Variational Generation
Paper and Code
Mar 28, 2017
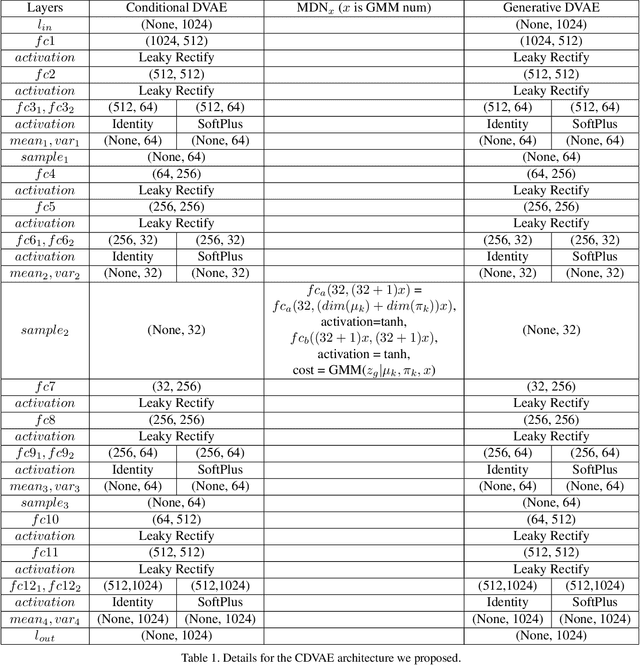
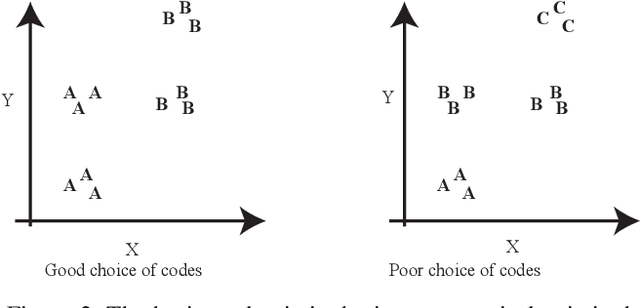
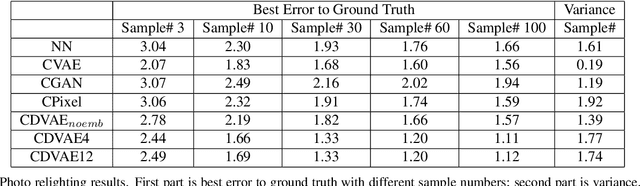
Problems such as predicting a new shading field (Y) for an image (X) are ambiguous: many very distinct solutions are good. Representing this ambiguity requires building a conditional model P(Y|X) of the prediction, conditioned on the image. Such a model is difficult to train, because we do not usually have training data containing many different shadings for the same image. As a result, we need different training examples to share data to produce good models. This presents a danger we call "code space collapse" - the training procedure produces a model that has a very good loss score, but which represents the conditional distribution poorly. We demonstrate an improved method for building conditional models by exploiting a metric constraint on training data that prevents code space collapse. We demonstrate our model on two example tasks using real data: image saturation adjustment, image relighting. We describe quantitative metrics to evaluate ambiguous generation results. Our results quantitatively and qualitatively outperform different strong baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge