CD-split: efficient conformal regions in high dimensions

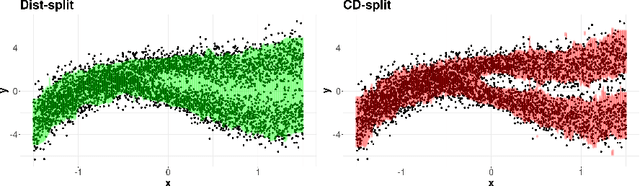
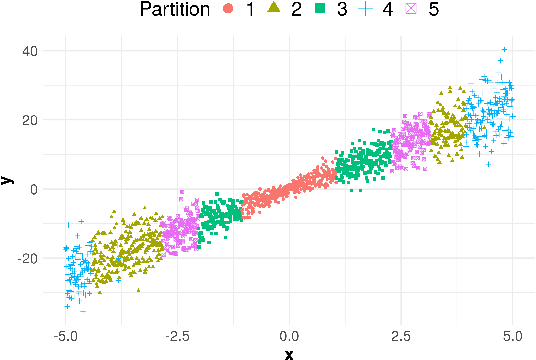
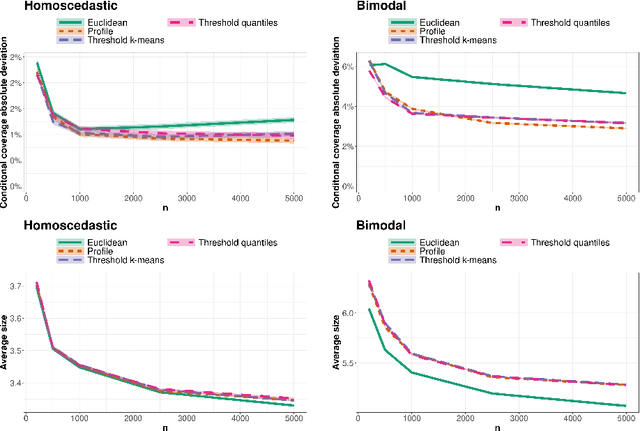
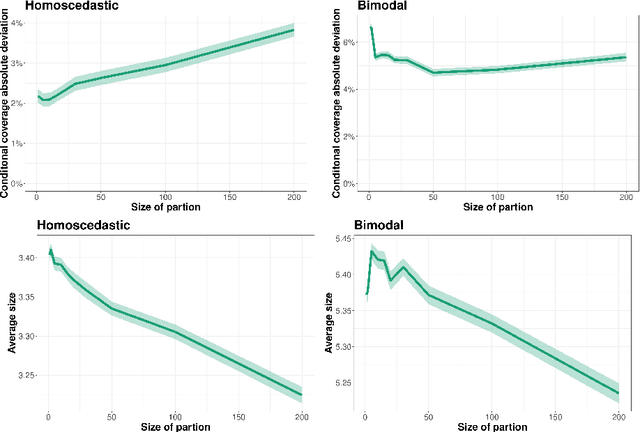
Conformal methods create prediction bands that control average coverage assuming solely i.i.d. data. Although the literature has mostly focused on prediction intervals, more general regions can often better represent uncertainty. For instance, a bimodal target is better represented by the union of two intervals. Such prediction regions are obtained by CD-split, which combines the split method and a data-driven partition of the feature space which scales to high dimensions. In this paper, we provide new theoretical properties and simulations related to CD-split. We show that CD-split converges asymptotically to the oracle highest density set. In particular, we show that CD-split satisfies local and asymptotic conditional validity. We also present many new simulations, which show how to tune CD-split and compare it to other methods in the literature. In a wide variety of these simulations, CD-split has a better conditional coverage and yields smaller prediction regions than other methods.