Causal effects based on distributional distances
Paper and Code
Jun 08, 2018

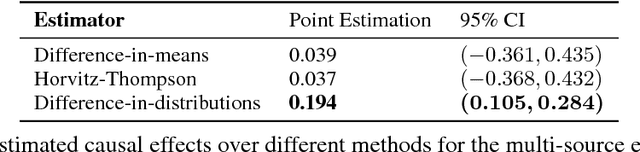

We develop a novel framework for estimating causal effects based on the discrepancy between unobserved counterfactual distributions. In our setting a causal effect is defined in terms of the $L_1$ distance between different counterfactual outcome distributions, rather than a mean difference in outcome values. Directly comparing counterfactual outcome distributions can provide more nuanced and valuable information about causality than a simple comparison of means. We consider single- and multi-source randomized studies, as well as observational studies, and analyze error bounds and asymptotic properties of the proposed estimators. We further propose methods to construct confidence intervals for the unknown mean distribution distance. Finally, we illustrate the new methods and verify their effectiveness in empirical studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge