Cascaded Gaussian Processes for Data-efficient Robot Dynamics Learning
Paper and Code
Oct 05, 2019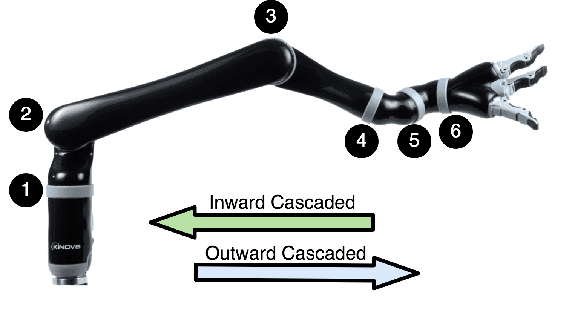
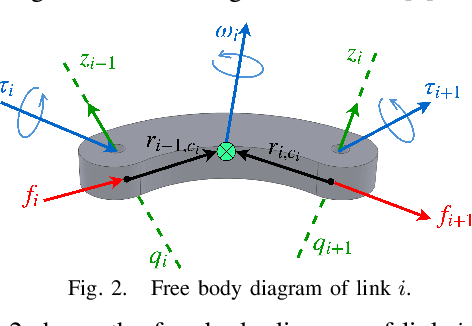
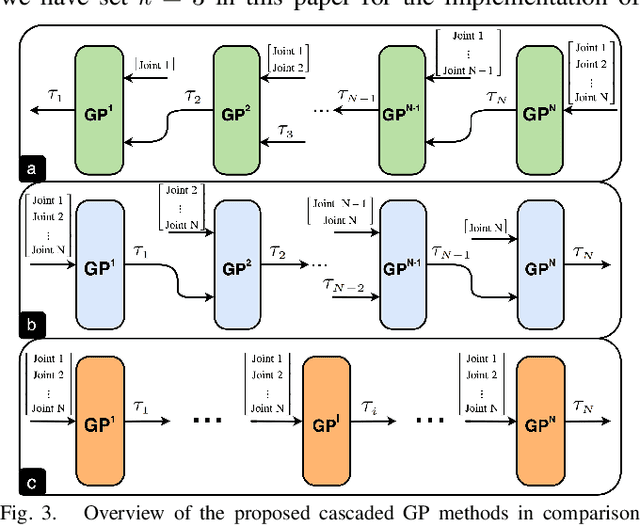
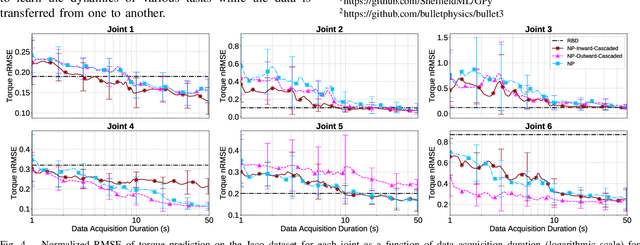
Motivated by the recursive Newton-Euler formulation, we propose a novel cascaded Gaussian process learning framework for the inverse dynamics of robot manipulators. This approach leads to a significant dimensionality reduction which in turn results in better learning and data efficiency. We explore two formulations for the cascading: the inward and outward, both along the manipulator chain topology. The learned modeling is tested in conjunction with the classical inverse dynamics model (semi-parametric) and on its own (non-parametric) in the context of feed-forward control of the arm. Experimental results are obtained with Jaco 2 six-DOF and SARCOS seven-DOF manipulators for randomly defined sinusoidal motions of the joints in order to evaluate the performance of cascading against the standard GP learning. In addition, experiments are conducted using Jaco 2 on a task emulating a pouring maneuver. Results indicate a consistent improvement in learning speed with the inward cascaded GP model and an overall improvement in data efficiency and generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge