CapProNet: Deep Feature Learning via Orthogonal Projections onto Capsule Subspaces

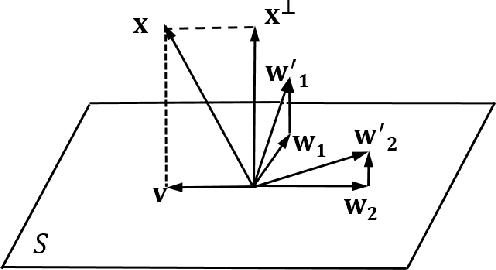
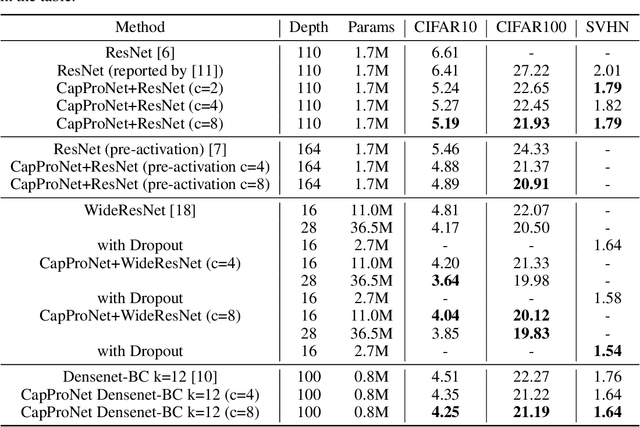
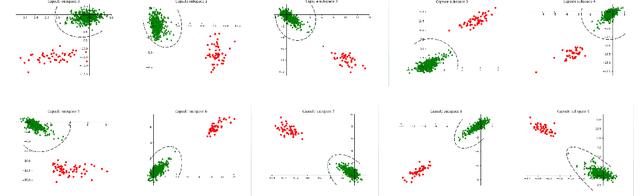
In this paper, we formalize the idea behind capsule nets of using a capsule vector rather than a neuron activation to predict the label of samples. To this end, we propose to learn a group of capsule subspaces onto which an input feature vector is projected. Then the lengths of resultant capsules are used to score the probability of belonging to different classes. We train such a Capsule Projection Network (CapProNet) by learning an orthogonal projection matrix for each capsule subspace, and show that each capsule subspace is updated until it contains input feature vectors corresponding to the associated class. We will also show that the capsule projection can be viewed as normalizing the multiple columns of the weight matrix simultaneously to form an orthogonal basis, which makes it more effective in incorporating novel components of input features to update capsule representations. In other words, the capsule projection can be viewed as a multi-dimensional weight normalization in capsule subspaces, where the conventional weight normalization is simply a special case of the capsule projection onto 1D lines. Only a small negligible computing overhead is incurred to train the network in low-dimensional capsule subspaces or through an alternative hyper-power iteration to estimate the normalization matrix. Experiment results on image datasets show the presented model can greatly improve the performance of the state-of-the-art ResNet backbones by $10-20\%$ and that of the Densenet by $5-7\%$ respectively at the same level of computing and memory expenses. The CapProNet establishes the competitive state-of-the-art performance for the family of capsule nets by significantly reducing test errors on the benchmark datasets.