Building powerful and equivariant graph neural networks with structural message-passing

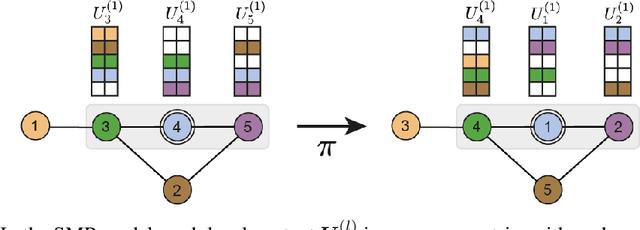
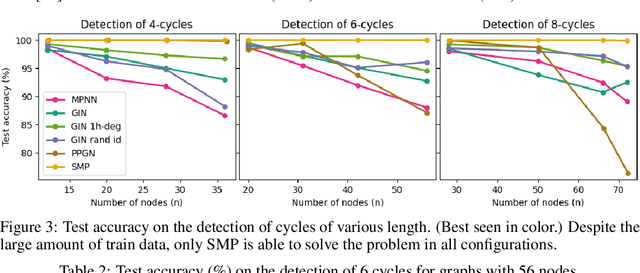
Message-passing has proved to be an effective way to design graph neural networks, as it is able to leverage both permutation equivariance and an inductive bias towards learning local structures to achieve good generalization. However, current message-passing architectures have a limited representation power and fail to learn basic topological properties of graphs. We address this problem and propose a new message-passing framework that is powerful while preserving permutation equivariance. Specifically, we propagate unique node identifiers in the form of a one-hot encoding in order to learn a local context matrix around each node. This enables to learn rich local information about both features and topology, which can be pooled to obtain node representations. Experimentally, we find our model to be superior at predicting various graph topological properties, opening the way to novel powerful architectures that are both equivariant and computationally efficient.