Branches: A Fast Dynamic Programming and Branch & Bound Algorithm for Optimal Decision Trees

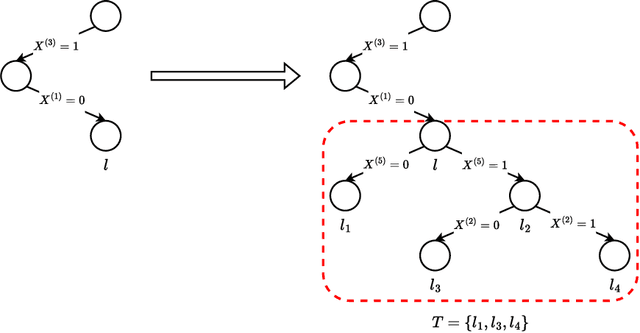
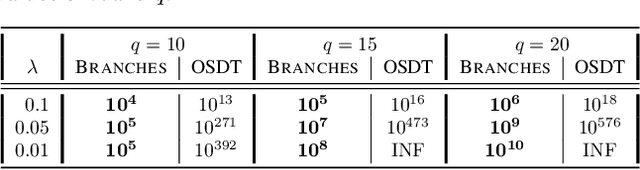
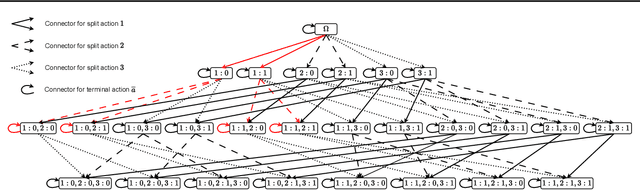
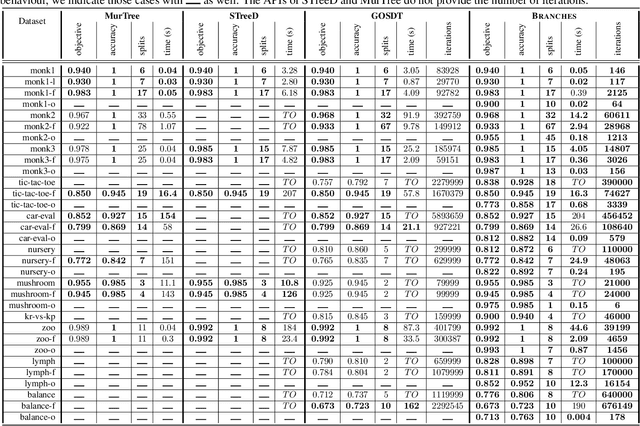
Decision Tree Learning is a fundamental problem for Interpretable Machine Learning, yet it poses a formidable optimization challenge. Despite numerous efforts dating back to the early 1990's, practical algorithms have only recently emerged, primarily leveraging Dynamic Programming (DP) and Branch & Bound (B&B) techniques. These breakthroughs led to the development of two distinct approaches. Algorithms like DL8.5 and MurTree operate on the space of nodes (or branches), they are very fast, but do not penalise complex Decision Trees, i.e. they do not solve for sparsity. On the other hand, algorithms like OSDT and GOSDT operate on the space of Decision Trees, they solve for sparsity but at the detriment of speed. In this work, we introduce Branches, a novel algorithm that integrates the strengths of both paradigms. Leveraging DP and B&B, Branches achieves exceptional speed while also solving for sparsity. Central to its efficiency is a novel analytical bound enabling substantial pruning of the search space. Theoretical analysis demonstrates that Branches has lower complexity compared to state-of-the-art methods, a claim validated through extensive empirical evaluation. Our results illustrate that Branches not only greatly outperforms existing approaches in terms of speed and number of iterations, it also consistently yields optimal Decision Trees.