Bounding data reconstruction attacks with the hypothesis testing interpretation of differential privacy
Paper and Code
Jul 08, 2023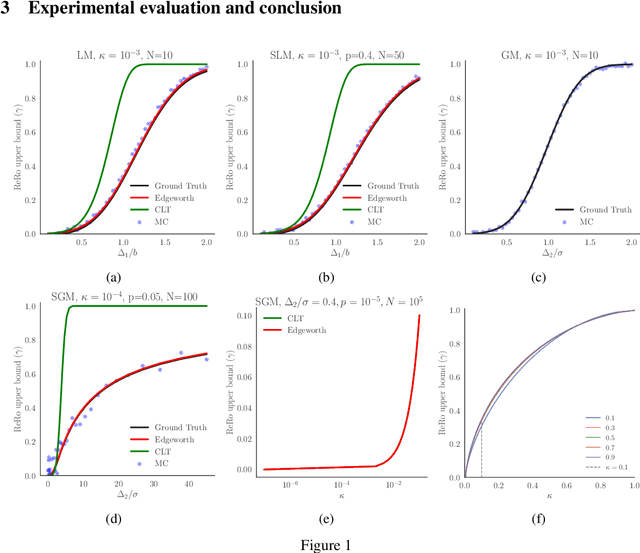
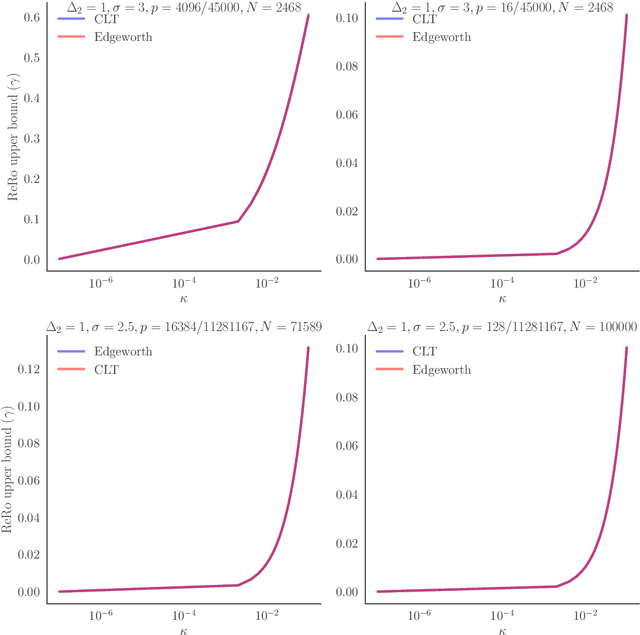
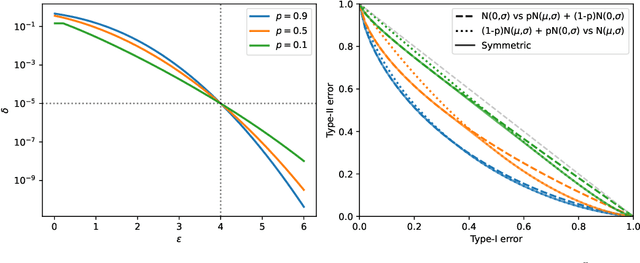
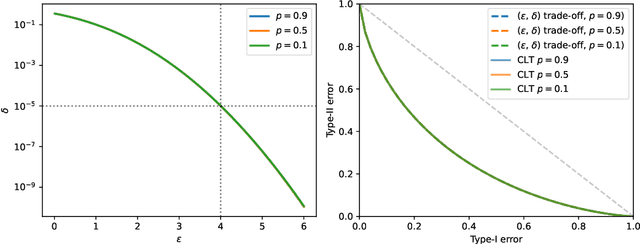
We explore Reconstruction Robustness (ReRo), which was recently proposed as an upper bound on the success of data reconstruction attacks against machine learning models. Previous research has demonstrated that differential privacy (DP) mechanisms also provide ReRo, but so far, only asymptotic Monte Carlo estimates of a tight ReRo bound have been shown. Directly computable ReRo bounds for general DP mechanisms are thus desirable. In this work, we establish a connection between hypothesis testing DP and ReRo and derive closed-form, analytic or numerical ReRo bounds for the Laplace and Gaussian mechanisms and their subsampled variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge