Bloom Origami Assays: Practical Group Testing
Paper and Code
Jul 21, 2020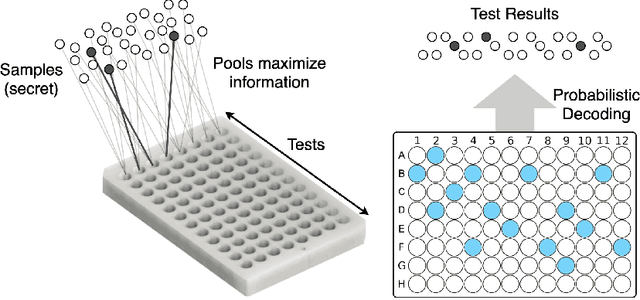
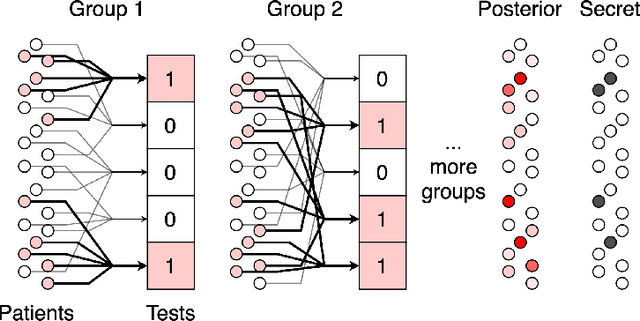
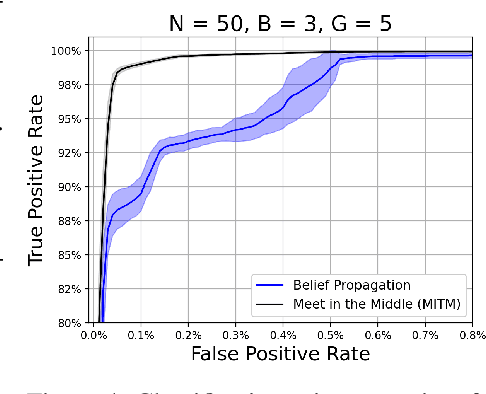
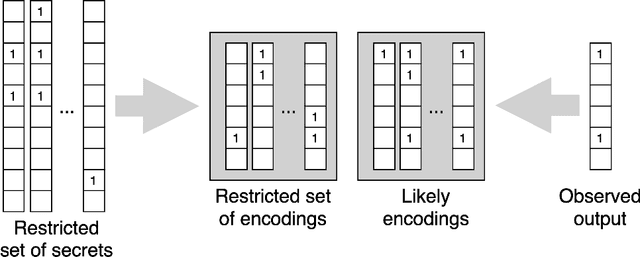
We study the problem usually referred to as group testing in the context of COVID-19. Given n samples collected from patients, how should we select and test mixtures of samples to maximize information and minimize the number of tests? Group testing is a well-studied problem with several appealing solutions, but recent biological studies impose practical constraints for COVID-19 that are incompatible with traditional methods. Furthermore, existing methods use unnecessarily restrictive solutions, which were devised for settings with more memory and compute constraints than the problem at hand. This results in poor utility. In the new setting, we obtain strong solutions for small values of n using evolutionary strategies. We then develop a new method combining Bloom filters with belief propagation to scale to larger values of n (more than 100) with good empirical results. We also present a more accurate decoding algorithm that is tailored for specific COVID-19 settings. This work demonstrates the practical gap between dedicated algorithms and well-known generic solutions. Our efforts results in a new and practical multiplex method yielding strong empirical performance without mixing more than a chosen number of patients into the same probe. Finally, we briefly discuss adaptive methods, casting them into the framework of adaptive sub-modularity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge