Block-Sparse Recovery Network for Two-Dimensional Harmonic Retrieval
Paper and Code
Nov 15, 2021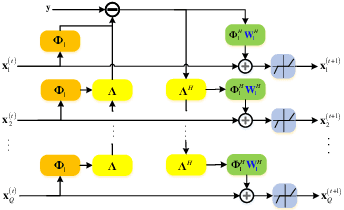

As a typical signal processing problem, multidimensional harmonic retrieval (MHR) has been adapted to a wide range of applications in signal processing. Block-sparse signals, whose nonzero entries appearing in clusters, have received much attention recently. An unfolded network, named Ada-BlockLISTA, was proposed to recover a block-sparse signal at a small computational cost, which learns an individual weight matrix for each block. However, as the number of network parameters is increasingly associated with the number of blocks, the demand for parameter reduction becomes very significant, especially for large-scale MHR. Based on the dictionary characteristics in two-dimensional (2D) harmonic retrieve problems, we introduce a weight coupling structure to shrink Ada-BlockLISTA, which significantly reduces the number of weights without performance degradation. In simulations, our proposed block-sparse reconstruction network, named AdaBLISTA-CP, shows excellent recovery performance and convergence speed in 2D harmonic retrieval problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge