Block-Diagonal and LT Codes for Distributed Computing With Straggling Servers
Paper and Code
Oct 19, 2018
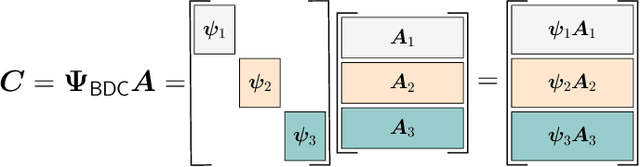
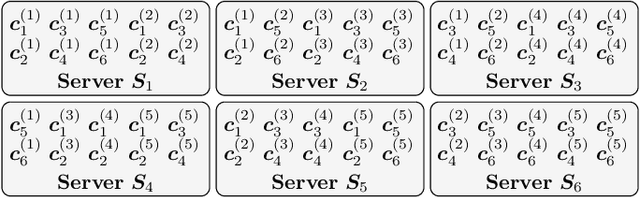
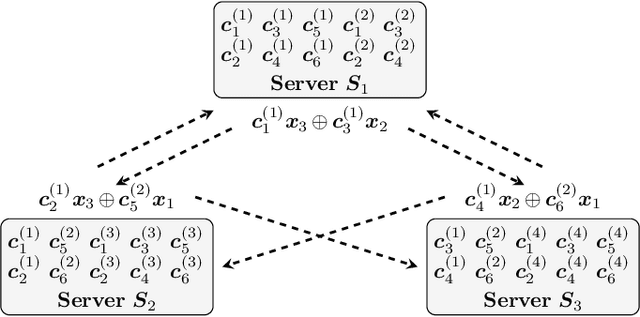
We propose two coded schemes for the distributed computing problem of multiplying a matrix by a set of vectors. The first scheme is based on partitioning the matrix into submatrices and applying maximum distance separable (MDS) codes to each submatrix. For this scheme, we prove that up to a given number of partitions the communication load and the computational delay (not including the encoding and decoding delay) are identical to those of the scheme recently proposed by Li et al., based on a single, long MDS code. However, due to the use of shorter MDS codes, our scheme yields a significantly lower overall computational delay when the delay incurred by encoding and decoding is also considered. We further propose a second coded scheme based on Luby Transform (LT) codes under inactivation decoding. Interestingly, LT codes may reduce the delay over the partitioned scheme at the expense of an increased communication load. We also consider distributed computing under a deadline and show numerically that the proposed schemes outperform other schemes in the literature, with the LT code-based scheme yielding the best performance for the scenarios considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge