Blending MPC & Value Function Approximation for Efficient Reinforcement Learning
Paper and Code
Dec 10, 2020
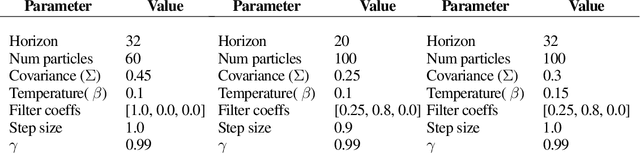
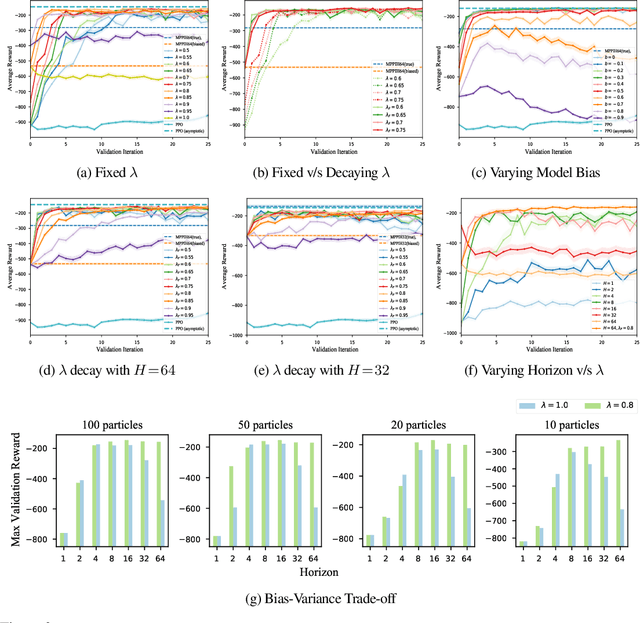
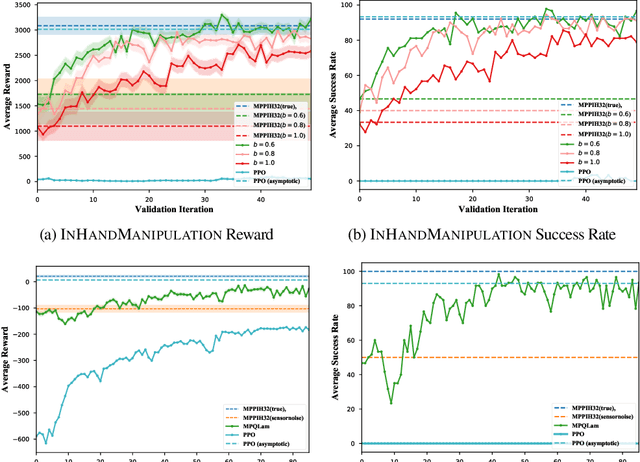
Model-Predictive Control (MPC) is a powerful tool for controlling complex, real-world systems that uses a model to make predictions about future behavior. For each state encountered, MPC solves an online optimization problem to choose a control action that will minimize future cost. This is a surprisingly effective strategy, but real-time performance requirements warrant the use of simple models. If the model is not sufficiently accurate, then the resulting controller can be biased, limiting performance. We present a framework for improving on MPC with model-free reinforcement learning (RL). The key insight is to view MPC as constructing a series of local Q-function approximations. We show that by using a parameter $\lambda$, similar to the trace decay parameter in TD($\lambda$), we can systematically trade-off learned value estimates against the local Q-function approximations. We present a theoretical analysis that shows how error from inaccurate models in MPC and value function estimation in RL can be balanced. We further propose an algorithm that changes $\lambda$ over time to reduce the dependence on MPC as our estimates of the value function improve, and test the efficacy our approach on challenging high-dimensional manipulation tasks with biased models in simulation. We demonstrate that our approach can obtain performance comparable with MPC with access to true dynamics even under severe model bias and is more sample efficient as compared to model-free RL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge