Bistatic Information Fusion for Positioning and Tracking in Integrated Sensing and Communication

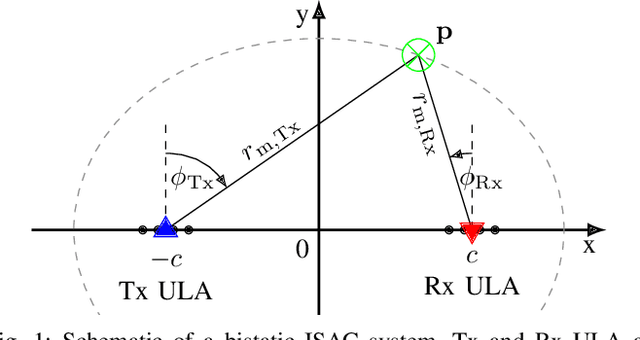
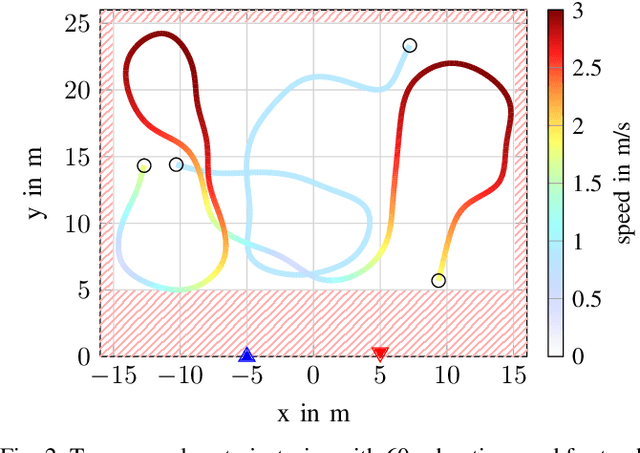
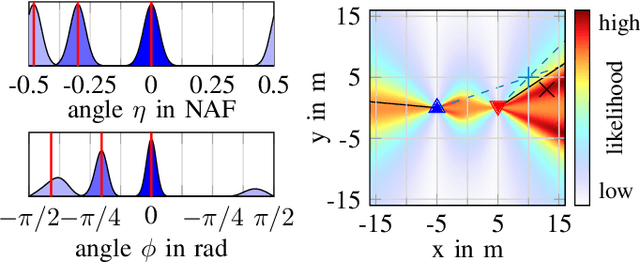
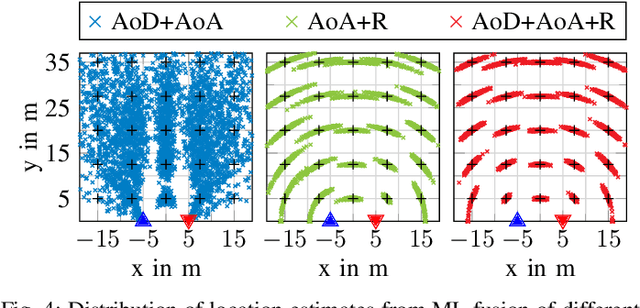
The distributed nature of cellular networks is one of the main enablers for integrated sensing and communication (ISAC). For target positioning and tracking, making use of bistatic measurements is non-trivial due to their non-linear relationship with Cartesian coordinates. Most of the literature proposes geometric-based methods to determine the target's location by solving a well-defined set of equations stemming from the available measurements. The error covariance to be used for Bayesian tracking is then derived from local Taylor expansions. In our work we adaptively fuse any subset of bistatic measurements using a maximum likelihood (ML) framework, allowing to incorporate every possible combination of available measurements, i.e., transmitter angle, receiver angle and bistatic range. Moreover, our ML approach is intrinsically flexible, as it can be extended to fuse an arbitrary number of measurements by multistatic setups. Finally, we propose both a fixed and dynamic way to compute the covariance matrix for the position error to be fed to Bayesian tracking techniques, like a Kalman filter. Numerical evaluations with realistic cellular communications parameters at mmWave frequencies show that our proposal outperforms the considered baselines, achieving a location and velocity root mean square error of 0.25 m and 0.83 m/s, respectively.