Bilevel Optimization for Feature Selection in the Data-Driven Newsvendor Problem
Paper and Code
Sep 12, 2022
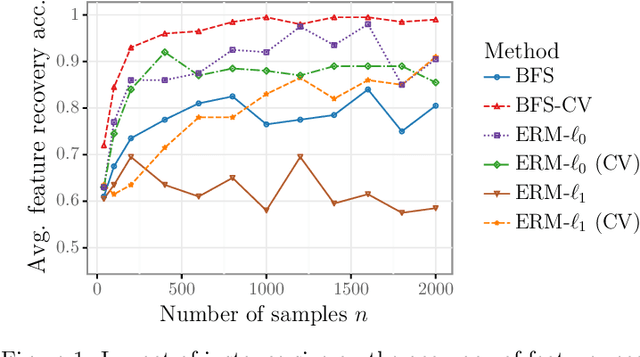
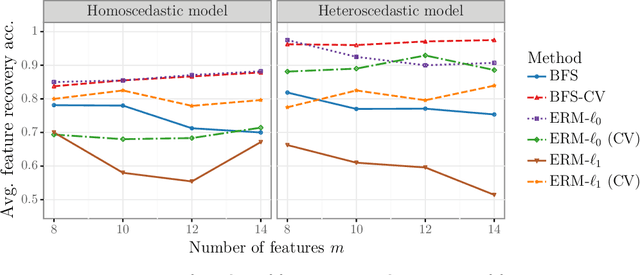
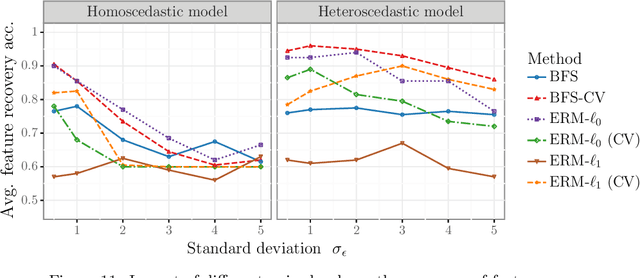
We study the feature-based newsvendor problem, in which a decision-maker has access to historical data consisting of demand observations and exogenous features. In this setting, we investigate feature selection, aiming to derive sparse, explainable models with improved out-of-sample performance. Up to now, state-of-the-art methods utilize regularization, which penalizes the number of selected features or the norm of the solution vector. As an alternative, we introduce a novel bilevel programming formulation. The upper-level problem selects a subset of features that minimizes an estimate of the out-of-sample cost of ordering decisions based on a held-out validation set. The lower-level problem learns the optimal coefficients of the decision function on a training set, using only the features selected by the upper-level. We present a mixed integer linear program reformulation for the bilevel program, which can be solved to optimality with standard optimization solvers. Our computational experiments show that the method accurately recovers ground-truth features already for instances with a sample size of a few hundred observations. In contrast, regularization-based techniques often fail at feature recovery or require thousands of observations to obtain similar accuracy. Regarding out-of-sample generalization, we achieve improved or comparable cost performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge