Bias of Homotopic Gradient Descent for the Hinge Loss
Paper and Code
Jul 26, 2019
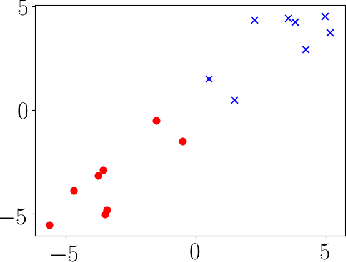
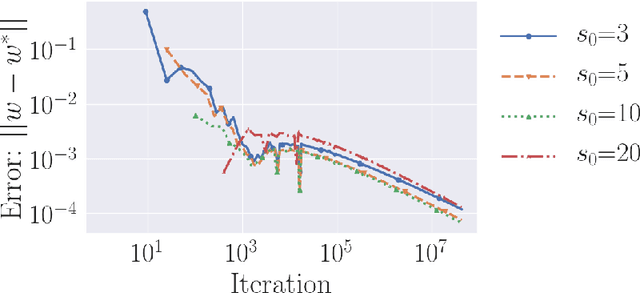
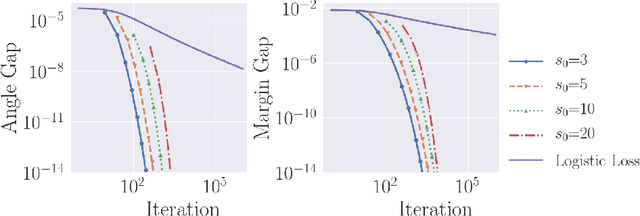
Gradient descent is a simple and widely used optimization method for machine learning. For homogeneous linear classifiers applied to separable data, gradient descent has been shown to converge to the maximal margin (or equivalently, the minimal norm) solution for various smooth loss functions. The previous theory does not, however, apply to non-smooth functions such as the hinge loss which is widely used in practice. Here, we study the convergence of a homotopic variant of gradient descent applied to the hinge loss and provide explicit convergence rates to the max-margin solution for linearly separable data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge