Beyond Worst-case Attacks: Robust RL with Adaptive Defense via Non-dominated Policies

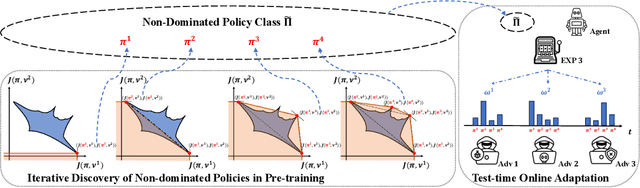
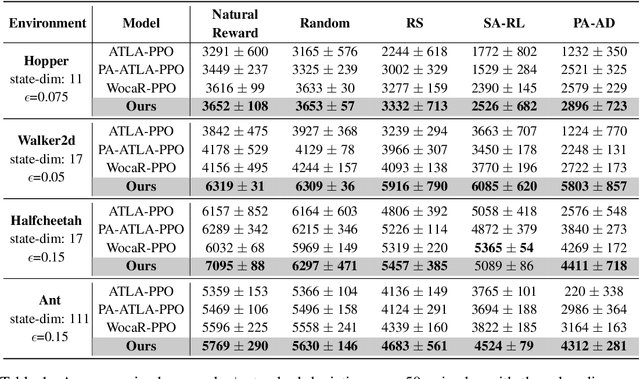
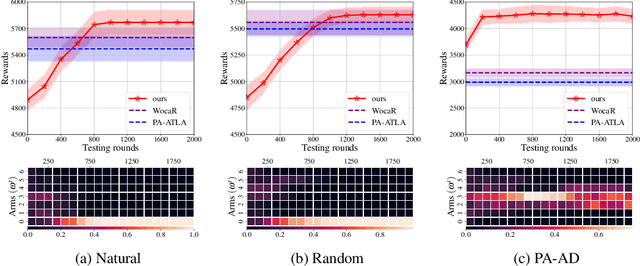
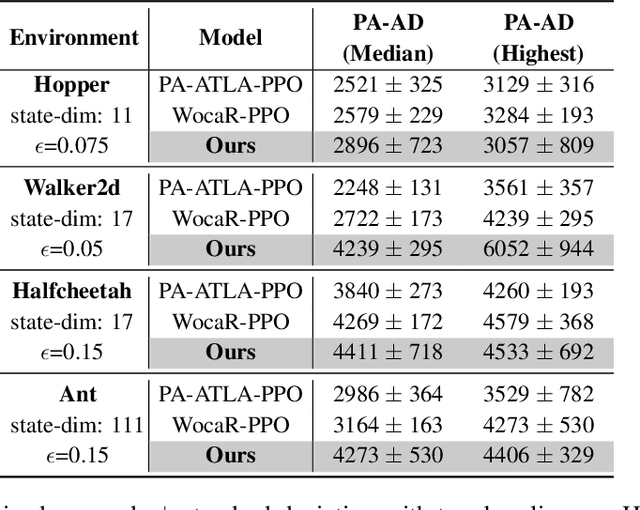
In light of the burgeoning success of reinforcement learning (RL) in diverse real-world applications, considerable focus has been directed towards ensuring RL policies are robust to adversarial attacks during test time. Current approaches largely revolve around solving a minimax problem to prepare for potential worst-case scenarios. While effective against strong attacks, these methods often compromise performance in the absence of attacks or the presence of only weak attacks. To address this, we study policy robustness under the well-accepted state-adversarial attack model, extending our focus beyond only worst-case attacks. We first formalize this task at test time as a regret minimization problem and establish its intrinsic hardness in achieving sublinear regret when the baseline policy is from a general continuous policy class, $\Pi$. This finding prompts us to \textit{refine} the baseline policy class $\Pi$ prior to test time, aiming for efficient adaptation within a finite policy class $\Tilde{\Pi}$, which can resort to an adversarial bandit subroutine. In light of the importance of a small, finite $\Tilde{\Pi}$, we propose a novel training-time algorithm to iteratively discover \textit{non-dominated policies}, forming a near-optimal and minimal $\Tilde{\Pi}$, thereby ensuring both robustness and test-time efficiency. Empirical validation on the Mujoco corroborates the superiority of our approach in terms of natural and robust performance, as well as adaptability to various attack scenarios.