Beyond Perturbation Stability: LP Recovery Guarantees for MAP Inference on Noisy Stable Instances
Paper and Code
Feb 26, 2021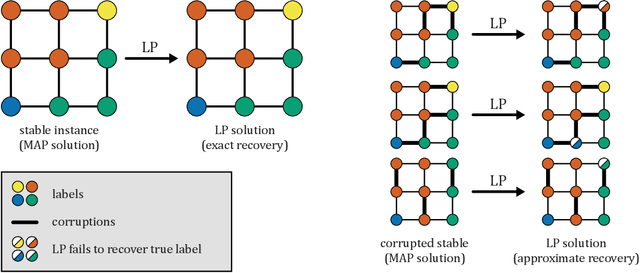


Several works have shown that perturbation stable instances of the MAP inference problem in Potts models can be solved exactly using a natural linear programming (LP) relaxation. However, most of these works give few (or no) guarantees for the LP solutions on instances that do not satisfy the relatively strict perturbation stability definitions. In this work, we go beyond these stability results by showing that the LP approximately recovers the MAP solution of a stable instance even after the instance is corrupted by noise. This "noisy stable" model realistically fits with practical MAP inference problems: we design an algorithm for finding "close" stable instances, and show that several real-world instances from computer vision have nearby instances that are perturbation stable. These results suggest a new theoretical explanation for the excellent performance of this LP relaxation in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge