Beyond Images: Label Noise Transition Matrix Estimation for Tasks with Lower-Quality Features

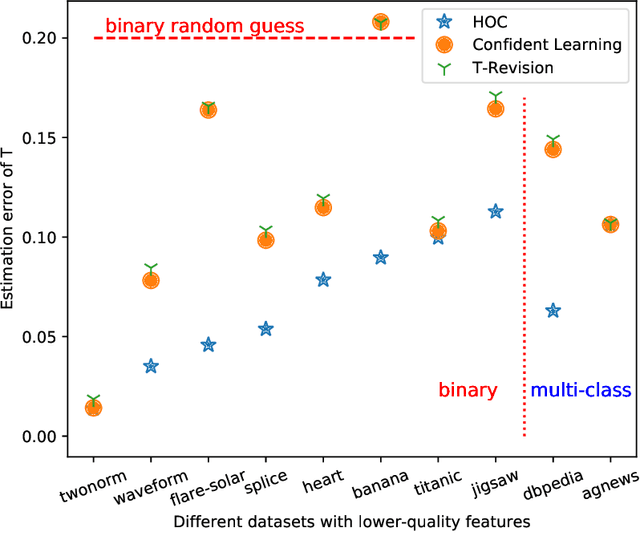
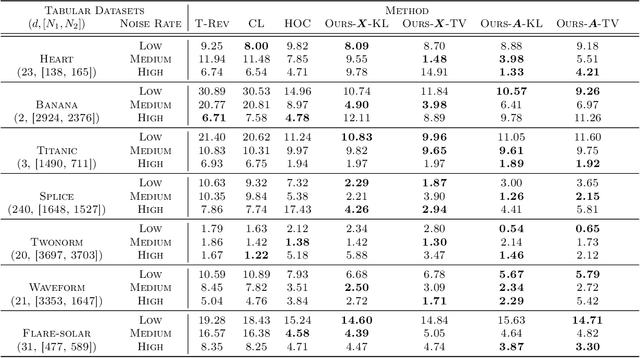
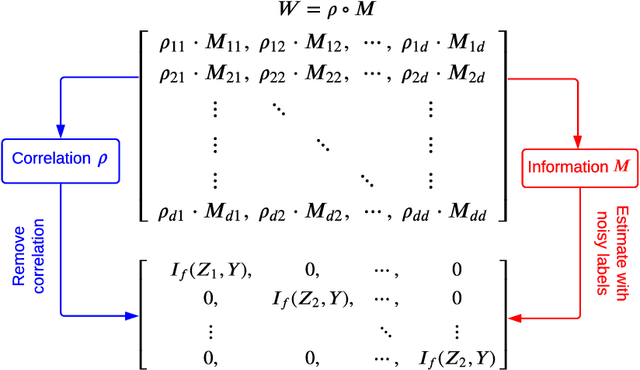
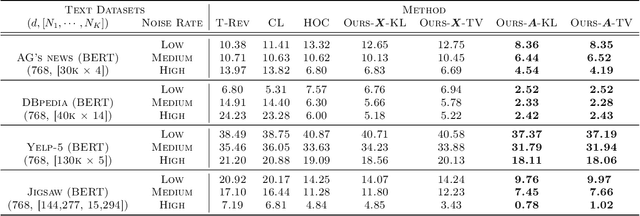
The label noise transition matrix, denoting the transition probabilities from clean labels to noisy labels, is crucial knowledge for designing statistically robust solutions. Existing estimators for noise transition matrices, e.g., using either anchor points or clusterability, focus on computer vision tasks that are relatively easier to obtain high-quality representations. However, for other tasks with lower-quality features, the uninformative variables may obscure the useful counterpart and make anchor-point or clusterability conditions hard to satisfy. We empirically observe the failures of these approaches on a number of commonly used datasets. In this paper, to handle this issue, we propose a generally practical information-theoretic approach to down-weight the less informative parts of the lower-quality features. The salient technical challenge is to compute the relevant information-theoretical metrics using only noisy labels instead of clean ones. We prove that the celebrated $f$-mutual information measure can often preserve the order when calculated using noisy labels. The necessity and effectiveness of the proposed method is also demonstrated by evaluating the estimation error on a varied set of tabular data and text classification tasks with lower-quality features. Code is available at github.com/UCSC-REAL/Est-T-MI.