BELT: Blockwise Missing Embedding Learning Transfomer

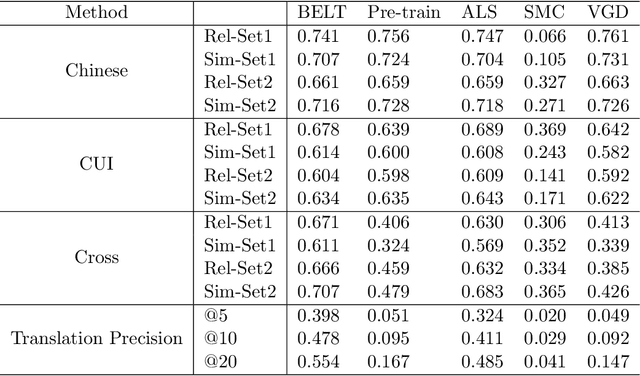
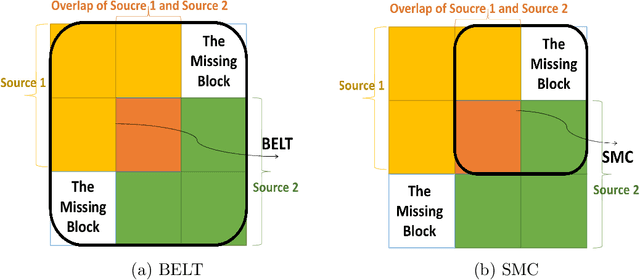
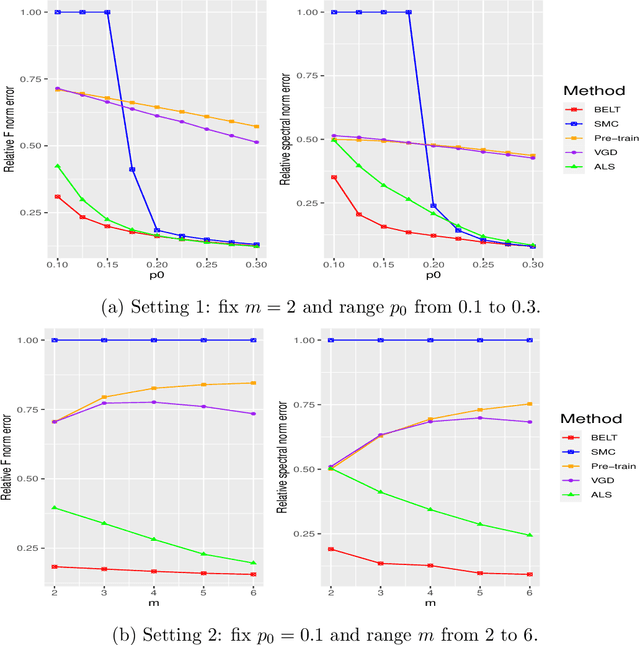
Matrix completion has attracted a lot of attention in many fields including statistics, applied mathematics and electrical engineering. Most of works focus on the independent sampling models under which the individual observed entries are sampled independently. Motivated by applications in the integration of multiple (point-wise mutual information) PMI matrices, we propose the model {\bf B}lockwise missing {\bf E}mbedding {\bf L}earning {\bf T}ransformer (BELT) to treat row-wise/column-wise missingness. Specifically, our proposed method aims at efficient matrix recovery when every pair of matrices from multiple sources has an overlap. We provide theoretical justification for the proposed BELT method. Simulation studies show that the method performs well in finite sample under a variety of configurations. The method is applied to integrate several PMI matrices built by EHR data and Chinese medical text data, which enables us to construct a comprehensive embedding set for CUI and Chinese with high quality.