Bayesian Topic Regression for Causal Inference
Paper and Code
Sep 11, 2021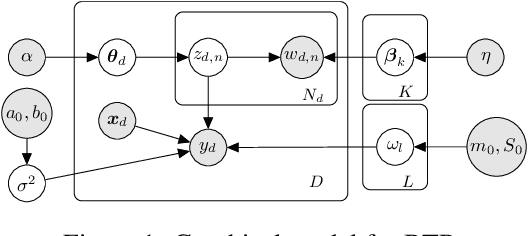
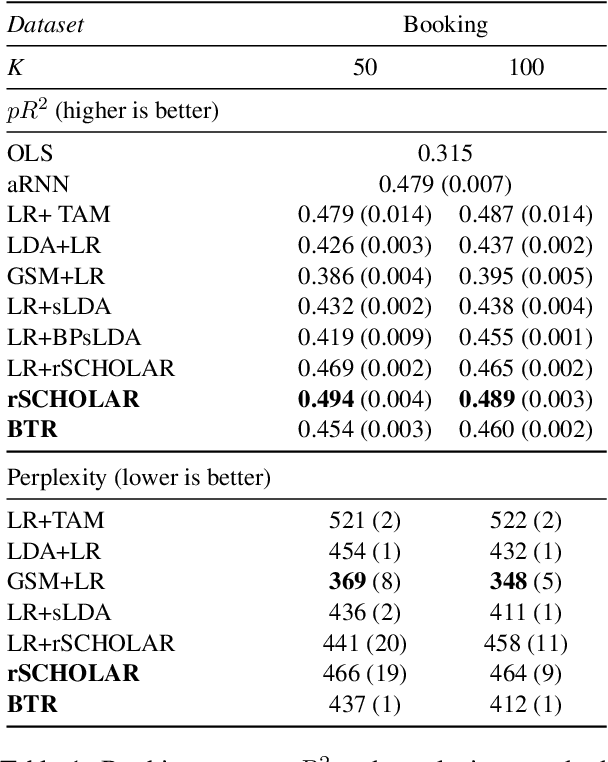
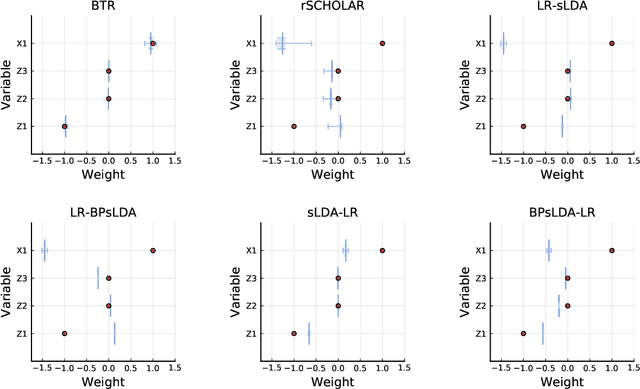
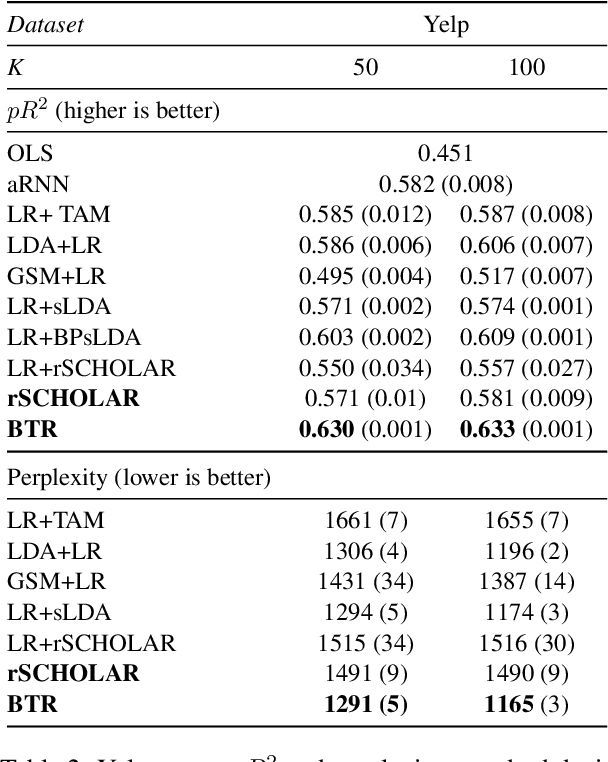
Causal inference using observational text data is becoming increasingly popular in many research areas. This paper presents the Bayesian Topic Regression (BTR) model that uses both text and numerical information to model an outcome variable. It allows estimation of both discrete and continuous treatment effects. Furthermore, it allows for the inclusion of additional numerical confounding factors next to text data. To this end, we combine a supervised Bayesian topic model with a Bayesian regression framework and perform supervised representation learning for the text features jointly with the regression parameter training, respecting the Frisch-Waugh-Lovell theorem. Our paper makes two main contributions. First, we provide a regression framework that allows causal inference in settings when both text and numerical confounders are of relevance. We show with synthetic and semi-synthetic datasets that our joint approach recovers ground truth with lower bias than any benchmark model, when text and numerical features are correlated. Second, experiments on two real-world datasets demonstrate that a joint and supervised learning strategy also yields superior prediction results compared to strategies that estimate regression weights for text and non-text features separately, being even competitive with more complex deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge