Bayesian Reinforcement Learning in Factored POMDPs
Paper and Code
Nov 14, 2018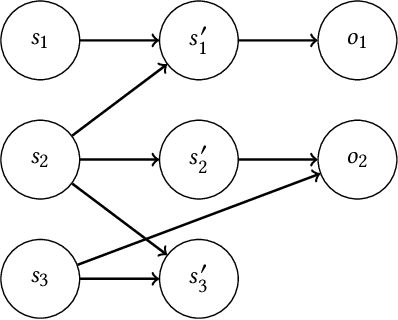

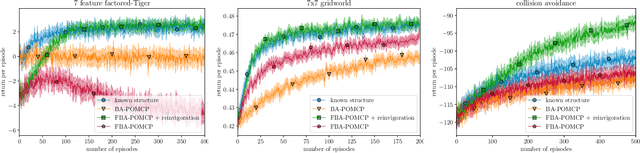

Bayesian approaches provide a principled solution to the exploration-exploitation trade-off in Reinforcement Learning. Typical approaches, however, either assume a fully observable environment or scale poorly. This work introduces the Factored Bayes-Adaptive POMDP model, a framework that is able to exploit the underlying structure while learning the dynamics in partially observable systems. We also present a belief tracking method to approximate the joint posterior over state and model variables, and an adaptation of the Monte-Carlo Tree Search solution method, which together are capable of solving the underlying problem near-optimally. Our method is able to learn efficiently given a known factorization or also learn the factorization and the model parameters at the same time. We demonstrate that this approach is able to outperform current methods and tackle problems that were previously infeasible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge